题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28题目解析:
思路一:排列组合
因为机器到底右下角,向下几步,向右几步都是固定的,
比如,m=3, n=2,我们只要向下 1 步,向右 2 步就一定能到达终点。即C(m-1,m+n-2)或者C(n-1,m+n-2);
思路二:动态规划
我们令 dp[i][j] 是到达 i, j 最多路径
动态方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]
注意,对于第一行 dp[0][j](0<=j<=n-1),或者第一列 dp[i][0](0<=i<=m-1),由于都是在边界,所以只能为 1
代码实现:
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}时间复杂度:O(m*n)
空间复杂度:O(m*n)
优化空间复杂度:由O(m*n)->O(n),时间复杂度还是O(m*n)
先初始化一个下面这样的表格,然后用左边的值加上上边的值就可以了
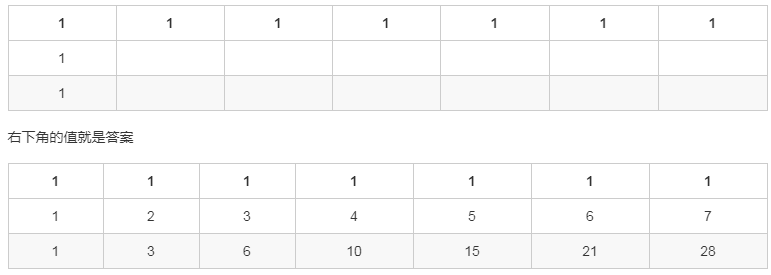
代码实现:
public static int uniquePaths(int m, int n) {
int arr[] = new int[n];
//填充数组arr
Arrays.fill(arr,1);
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
arr[j]+=arr[j-1];
}
}
return arr[n-1];
}
 IDEA激活码
IDEA激活码


