求最优子问题,动态规划和其它遍历算法(如深/广度优先搜索)都是将原问题拆成多个子问题然后求解。他们之间最本质的区别是,动态规划保存子问题的解(使用dp[]),避免重复计算。
动态规划的题型丰富多样,没有规律可循。但是它们的思想是一样的,这里给出作者总结的做题四个步骤,适用于所有动态规划
- 确认状态:开一个数组,一维二维都行。用来存储最优子问题。这里还要思考两点
- 最后一步:确定最后一步,整体问题就分为【最优子问题,最后一步】
- 子问题:将原问题转换成一个子问题,规模变小,假设这个子问题就是最优的。
- 转移方程:根据上面两个思考,求得转移方程f[x]=...
- 初始条件和边界条件:
- 初始条件比如:f[0]=0,用转移方程算不出来的,需要手动定义
- 边界情况:什么时候停下来,不要让数组越界
- 计算顺序:保证计算等式左边的时候,等式右边的数全部算完。一般都是从小到大,for循环搞定
动态方程适用于:计数,求最大值最小值,求存在性三类问题,下面按照这三类进行总结。
一.计数
滚动数组也可以看作动态规划的升级版,因为滚动数组的空间复杂度为O(1)。该题的动态规划只用到前2个数,就可以使用2个变量存储,而不是数组存储。
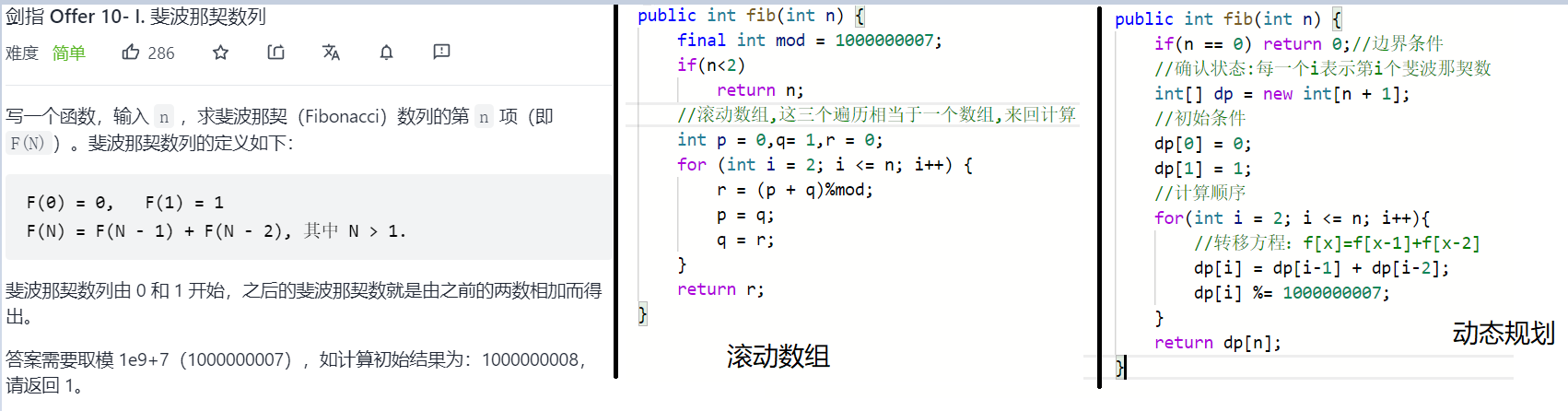
该题和"爬楼梯"是一模一样(基础版)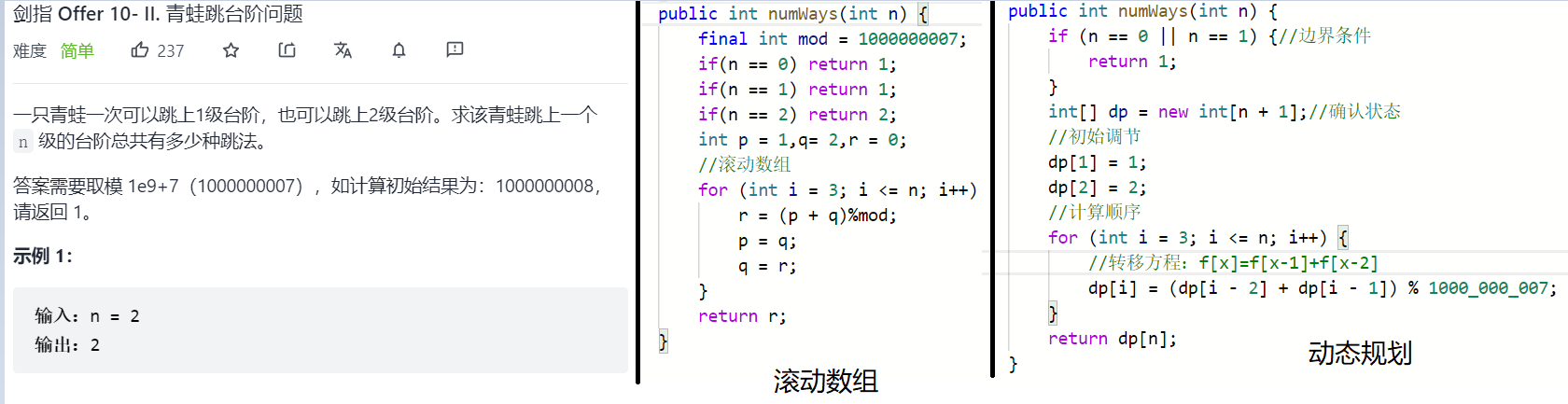
(升级版):根据不同的条件使用不同的转移方程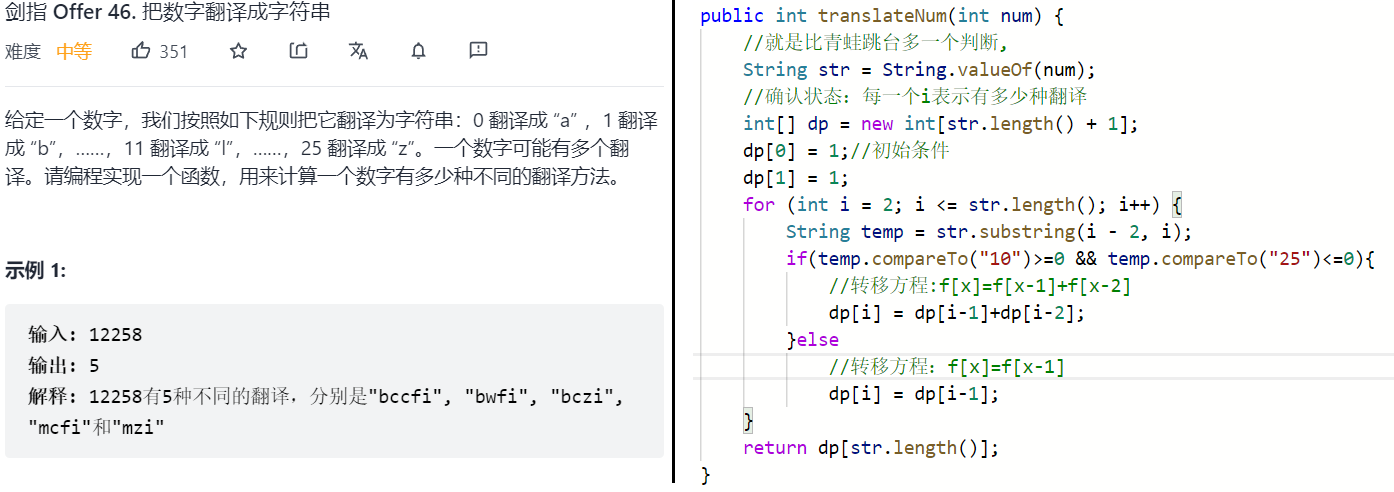
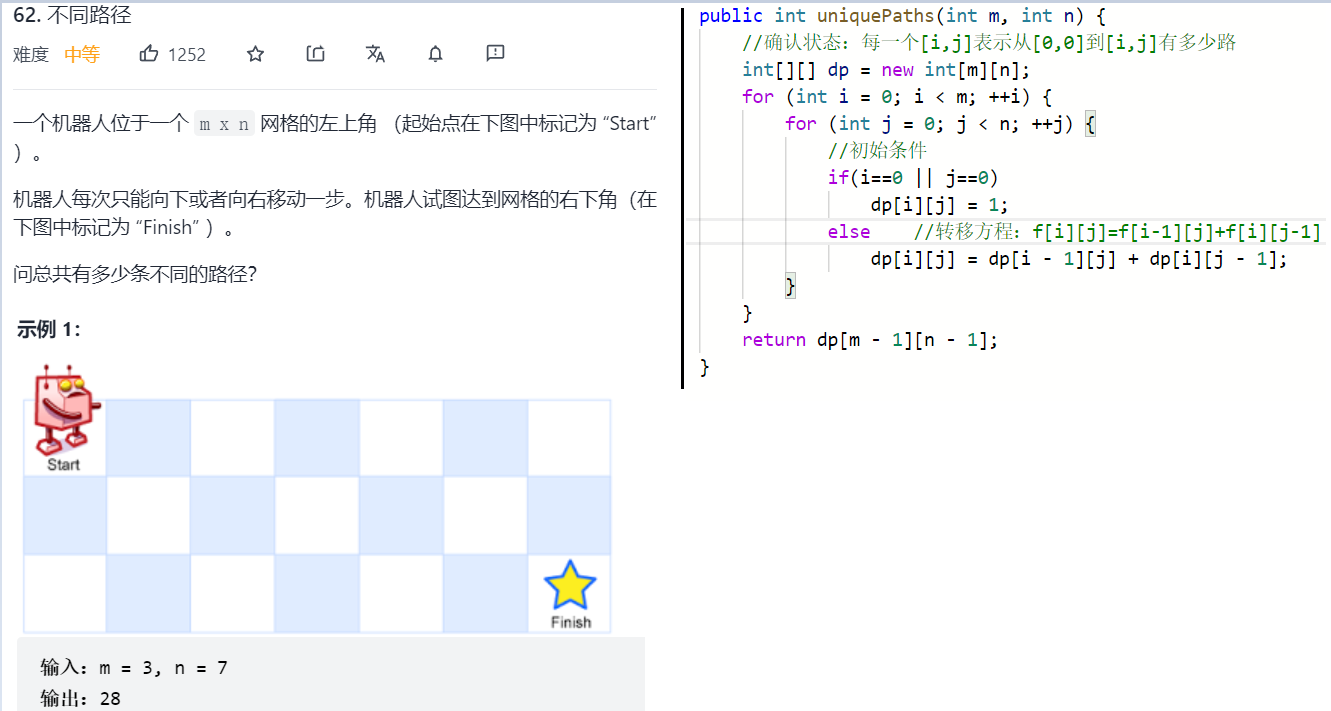
两种动态规划,使用的转移方程不同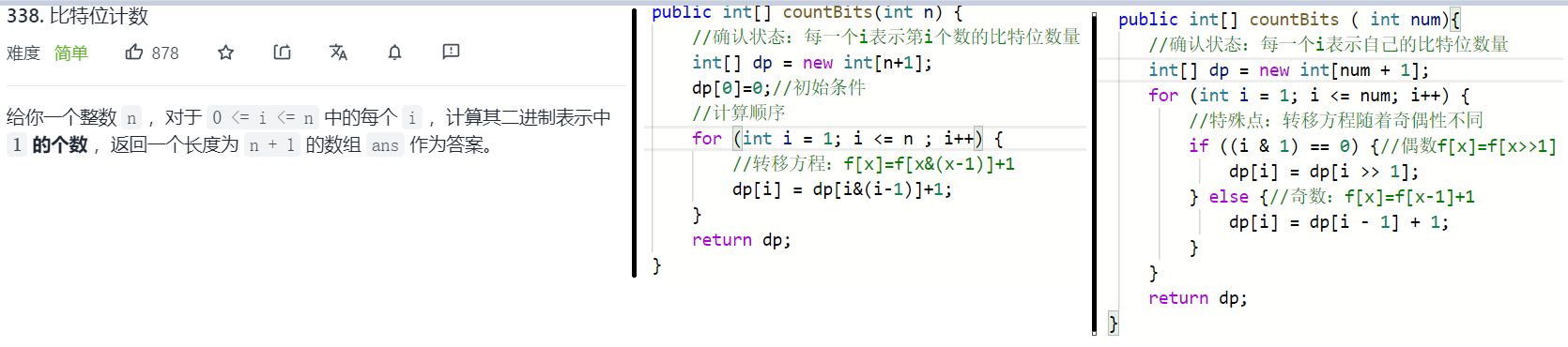
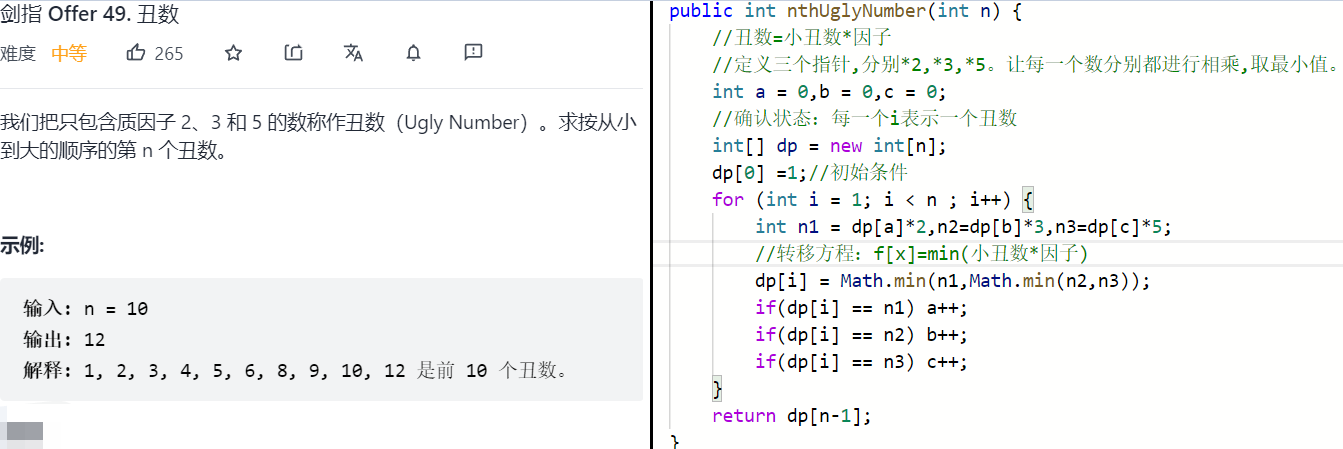
二.求最值
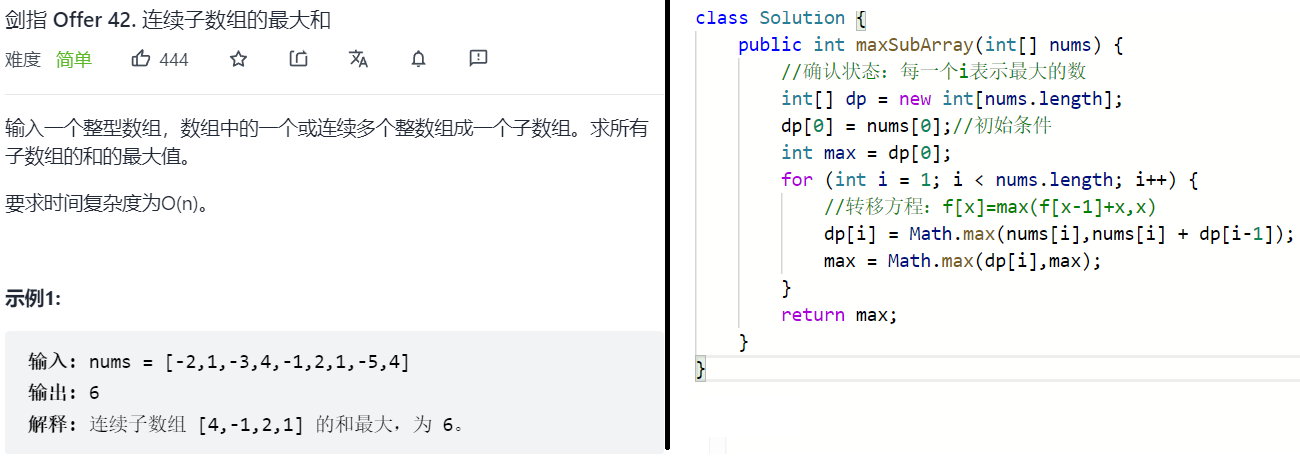
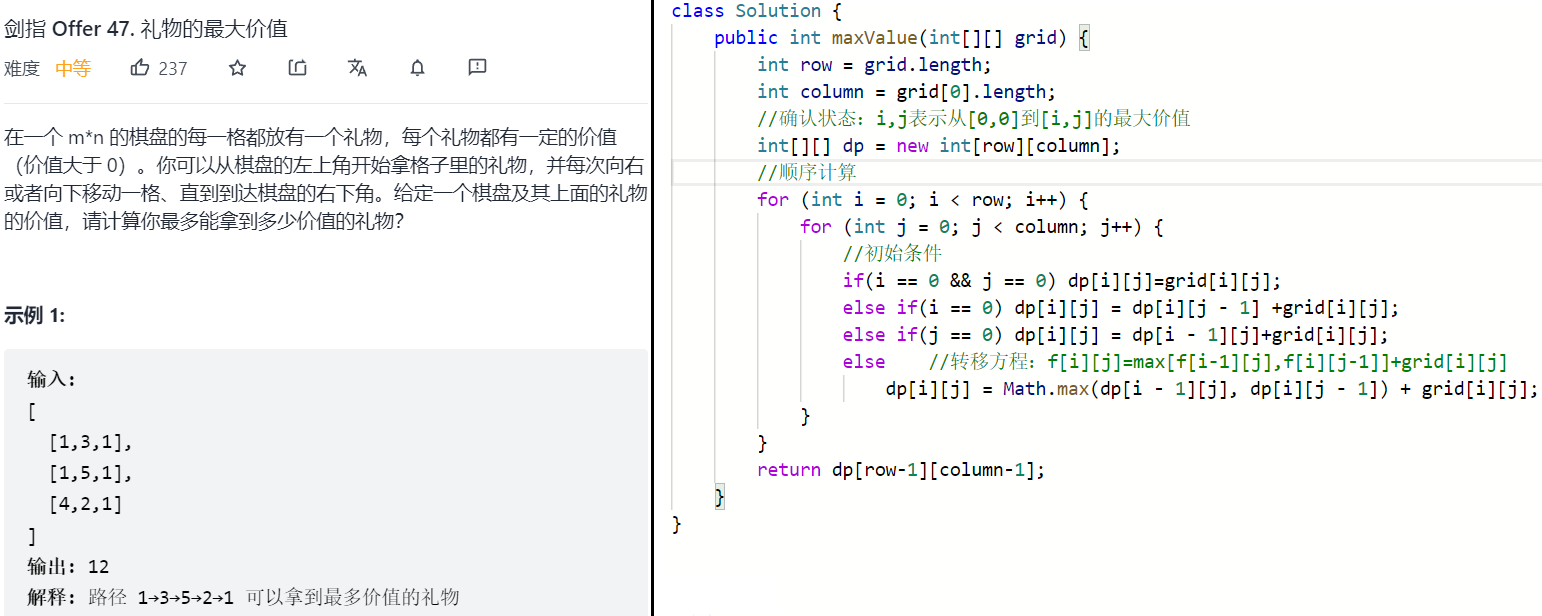
该题与上面题型一模一样,就是一个求最大,一个求最小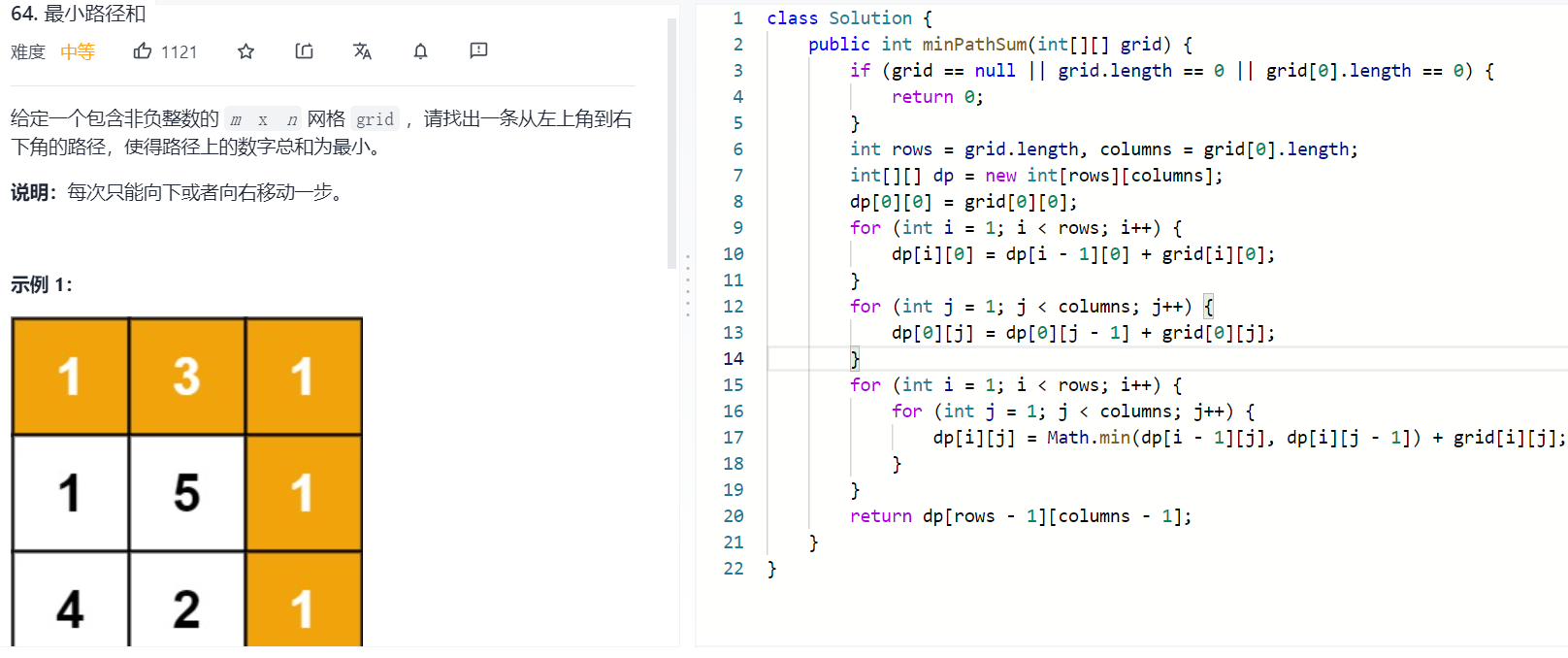
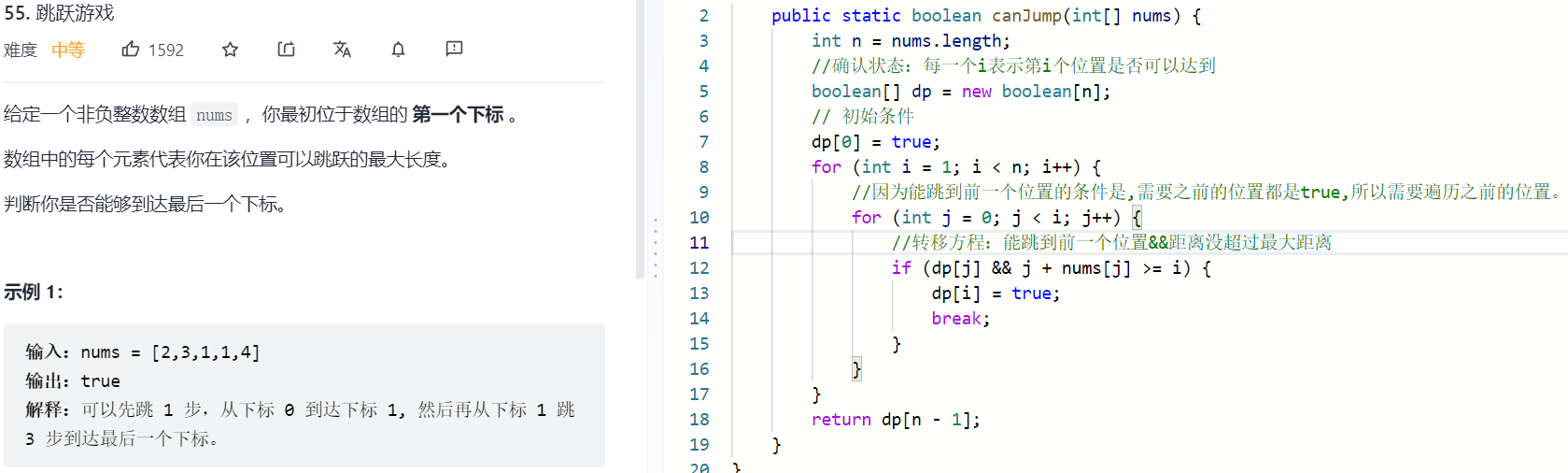
三.求存在性
该题使用贪心算法效率比较高,贪心算法后面专门放文章讲
寄语:世上只有一种英雄主义,就是在认清生活真相之后依然热爱生活。
 IDEA激活码
IDEA激活码


