指针三剑客之二：树

树作为（单）链表的升级版，我们通常接触的树都是二叉树（binary tree），即每个节点最多有两个子节点；

还有一种特殊的树：搜索二叉树，它是按照左小右大的顺序存放元素。

遍历树的时候可能会涉及深度优先搜索和广度优先搜索。不会的小伙伴可以查看我的"一切皆可搜索"。遍历树一般使用递归。

一.树的递归

树递归=深度优先搜索 ：树的递归是使用深度优先搜索的思想进行的

递归的本质是栈调用，所有递归都可以使用栈代替。

利用树递归求题无非两种：先深入再处理，先处理再深入。

• 先深入再处理：

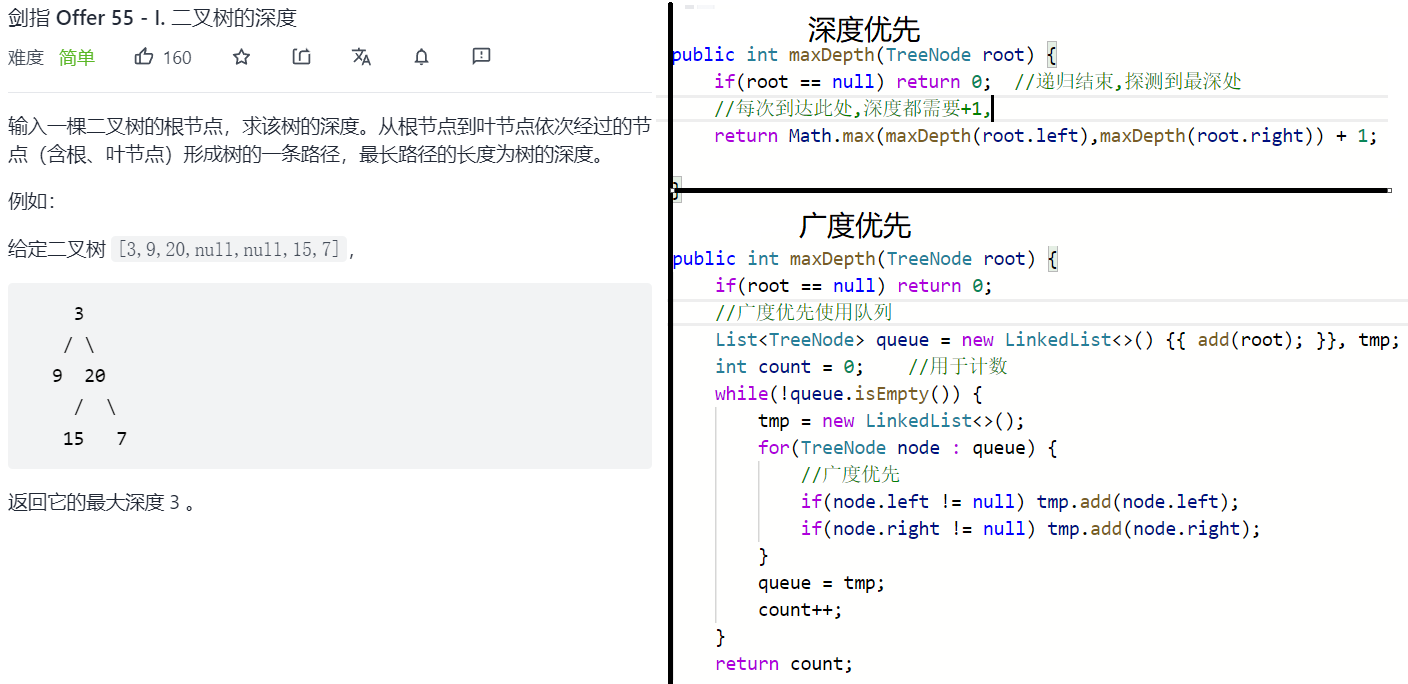
 平衡二叉树利用二叉树的深度求得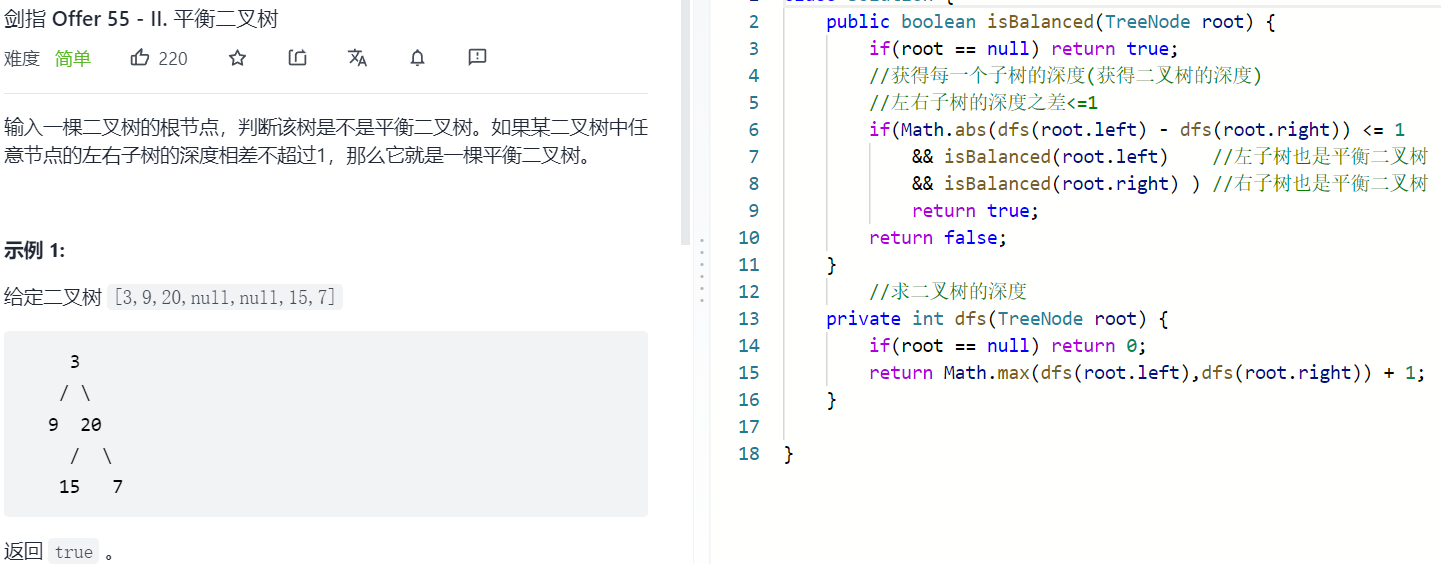

 该题就体现了所有的递归都可以用栈实现

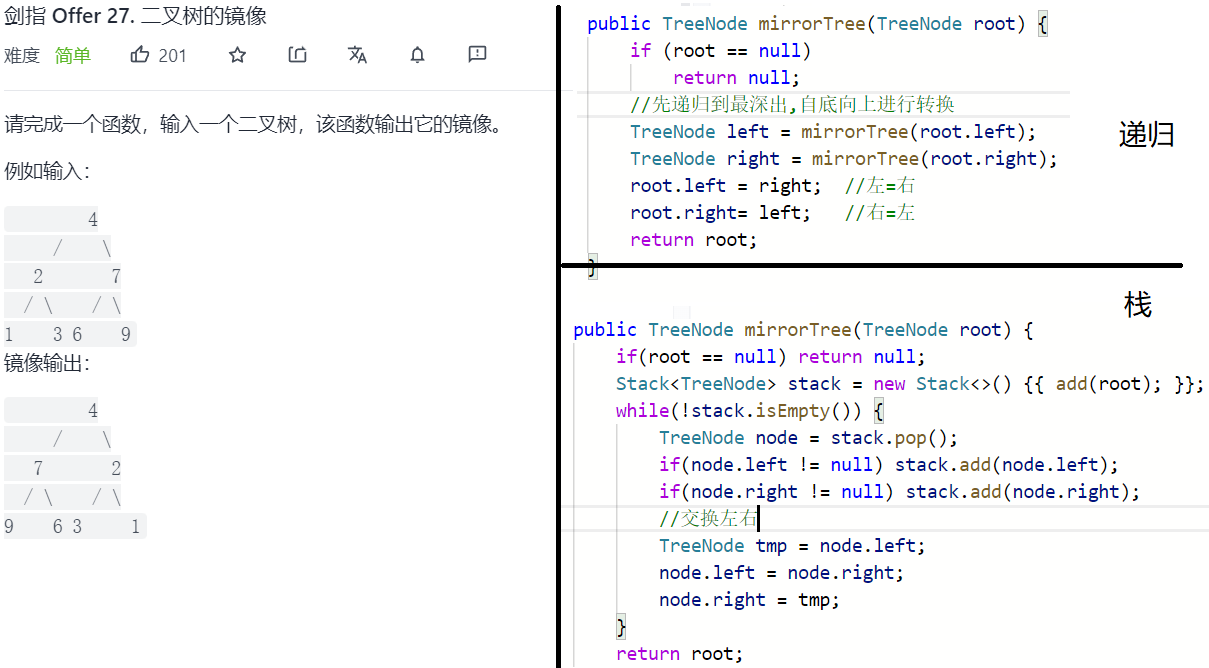
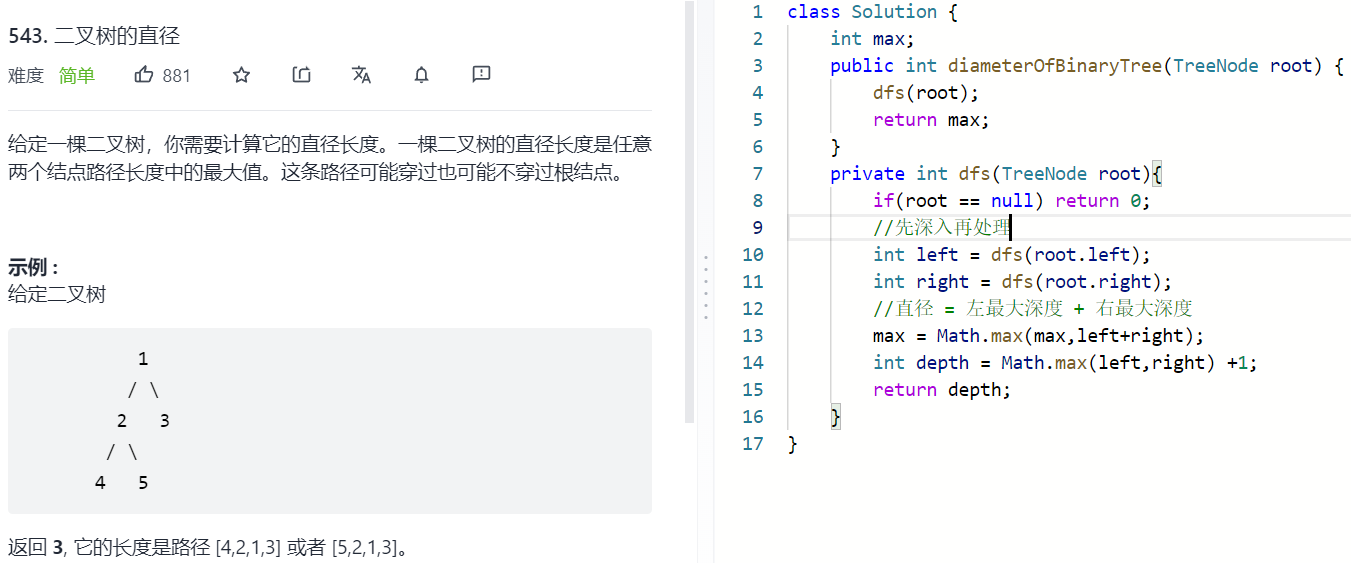
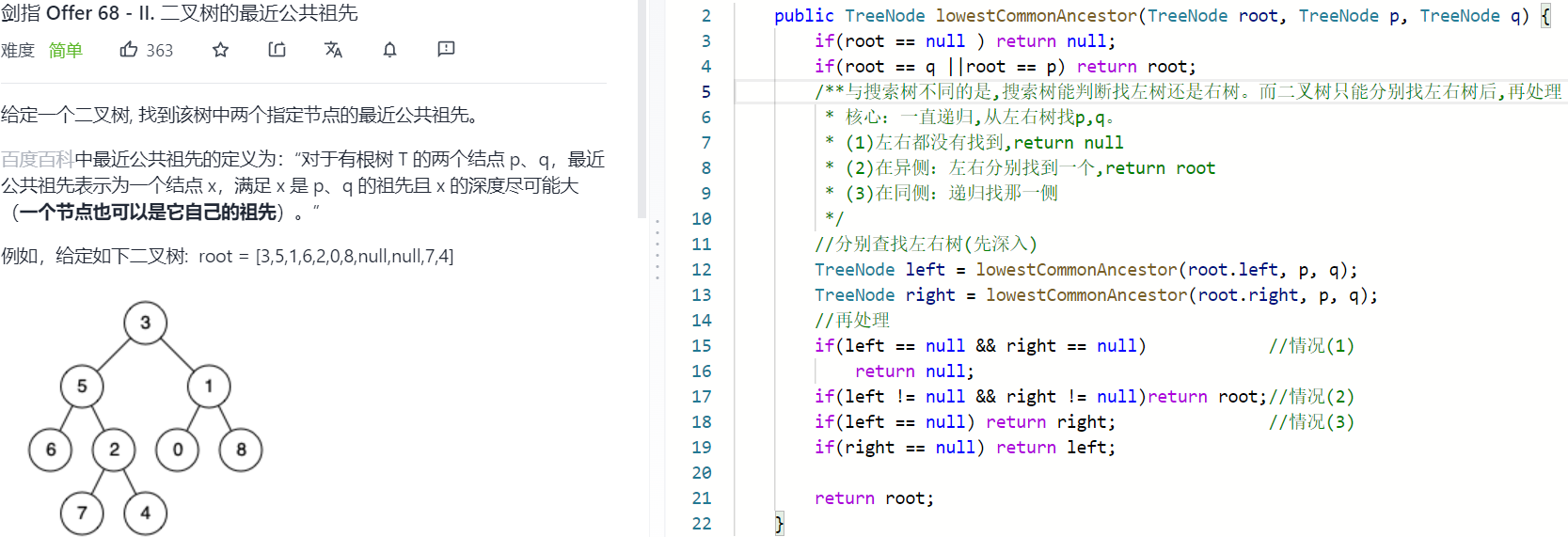
•  先处理再深入：

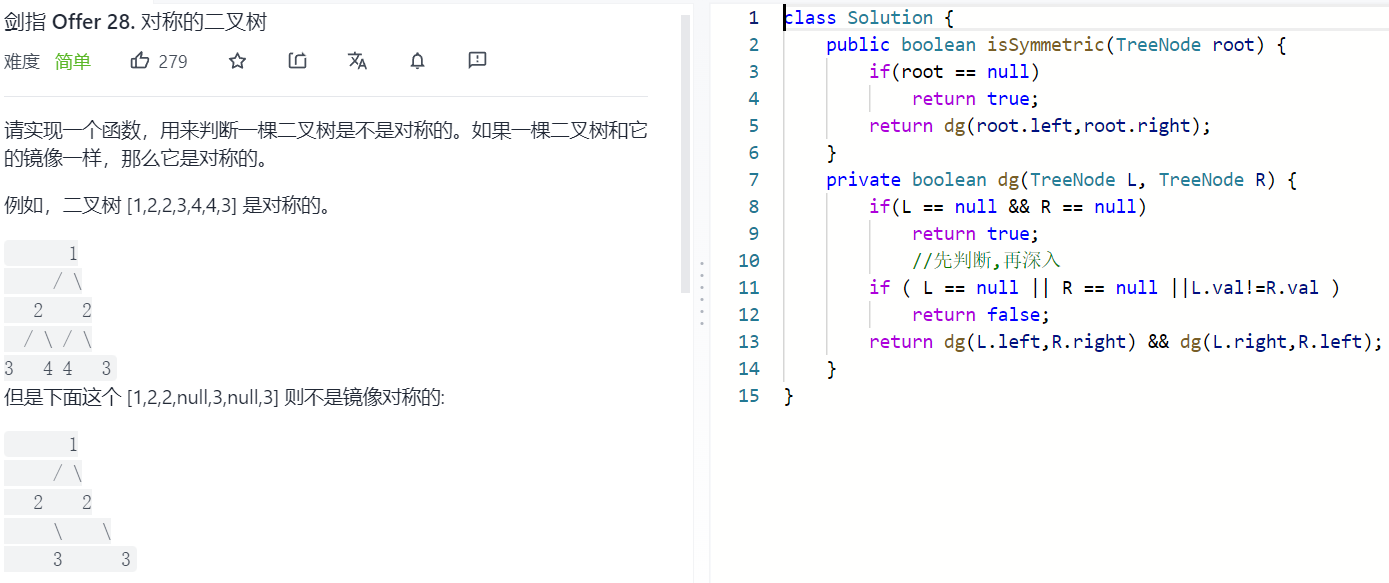
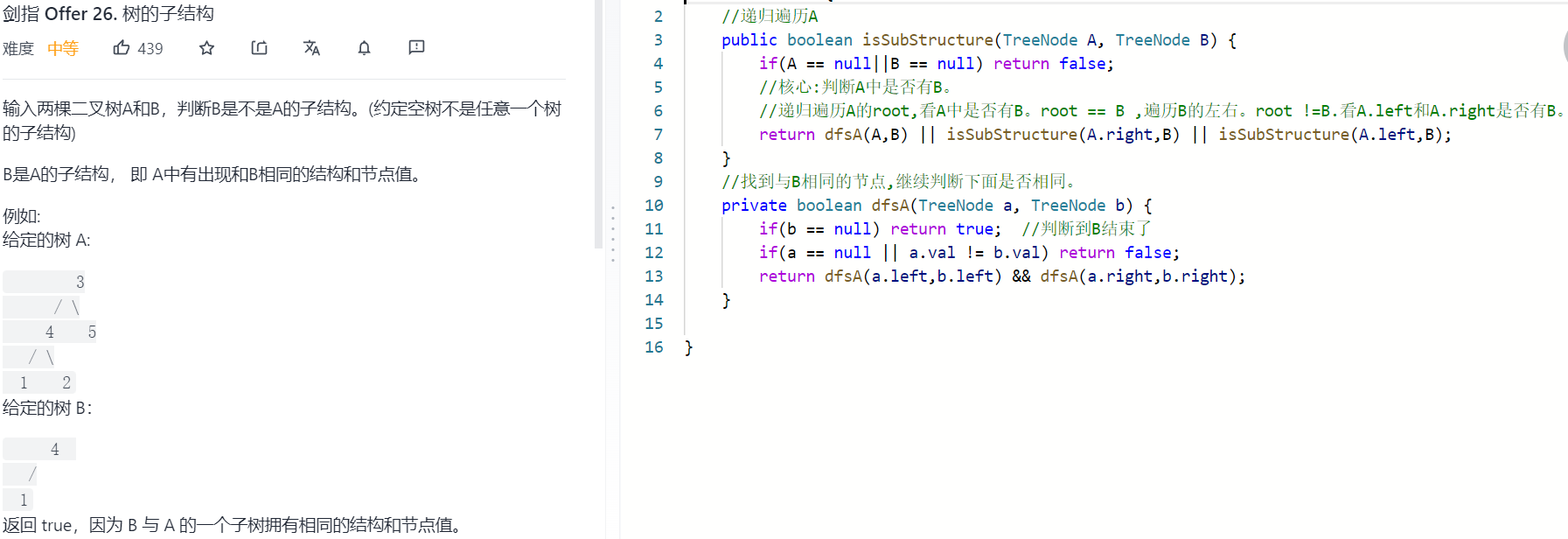
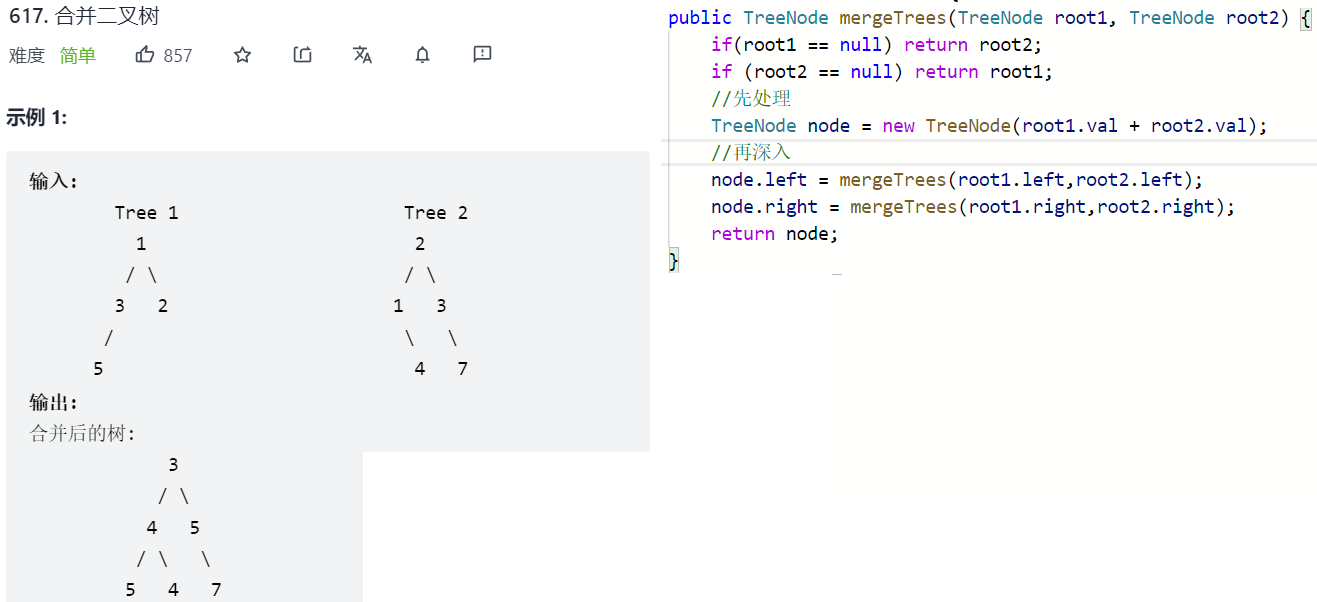
 二.层次遍历

层次遍历=广度优先搜索：层次遍历是使用广度优先搜索的思想进行的。

广度优先是使用队列实现的。

基础版

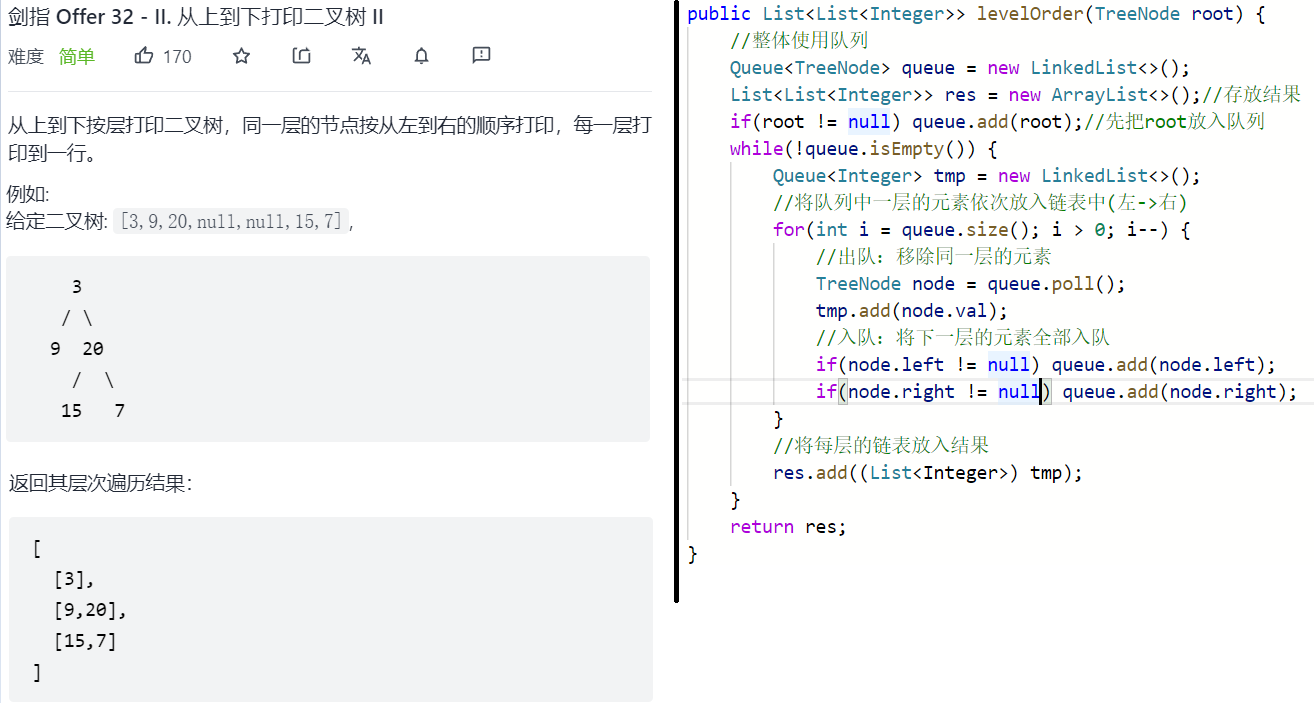
升级版：其实就是存储结果的时候，使用一个双端队列，让奇偶层存储的顺序不同，原本的顺序没有改变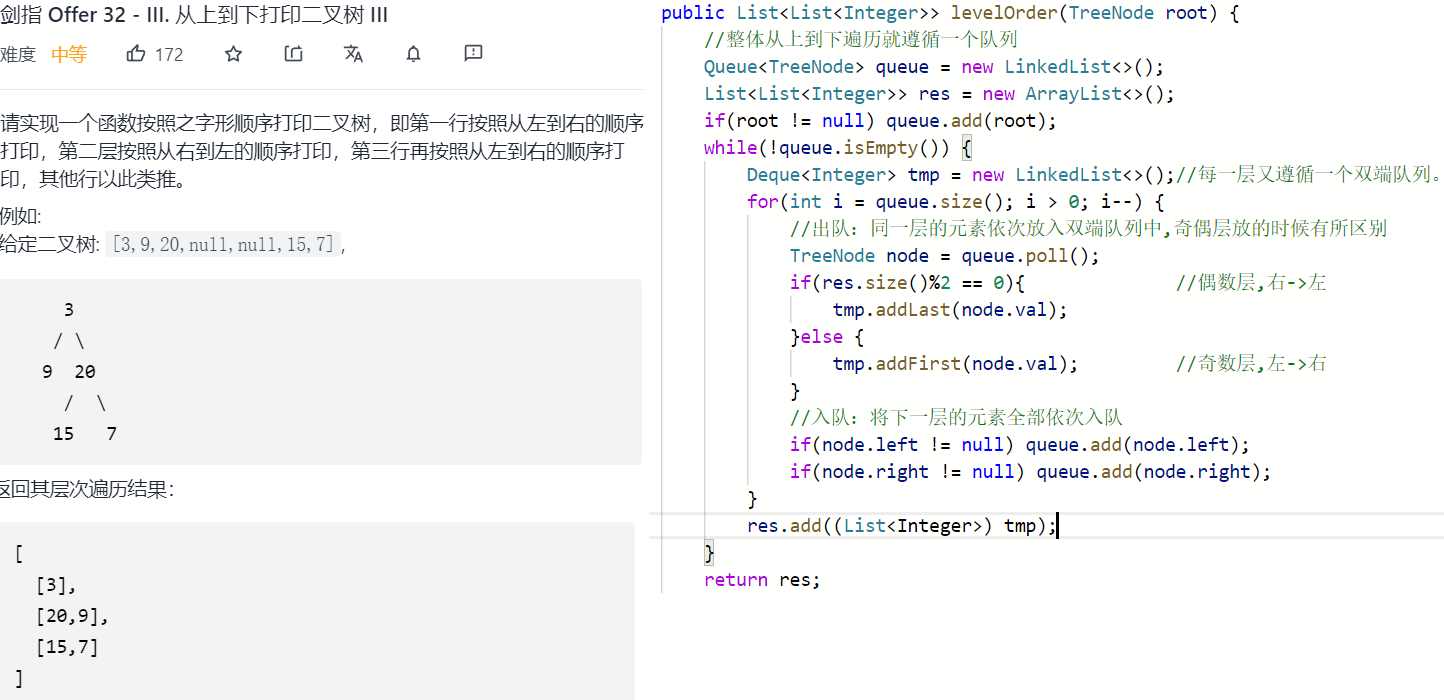

三.前中后序遍历

前中后序都是使用深度优先搜索

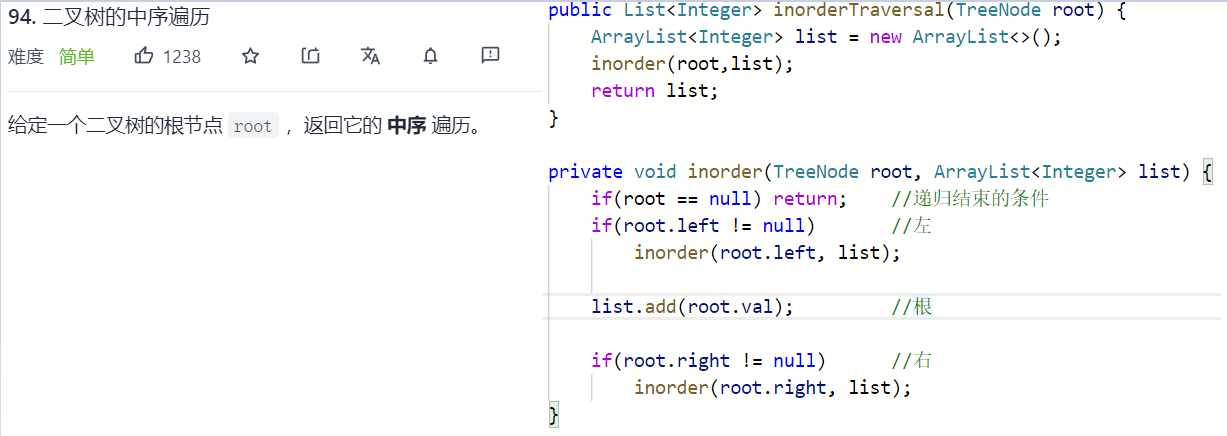
核心：根据前序遍历得到根节点，根据中序遍历区分左右子树。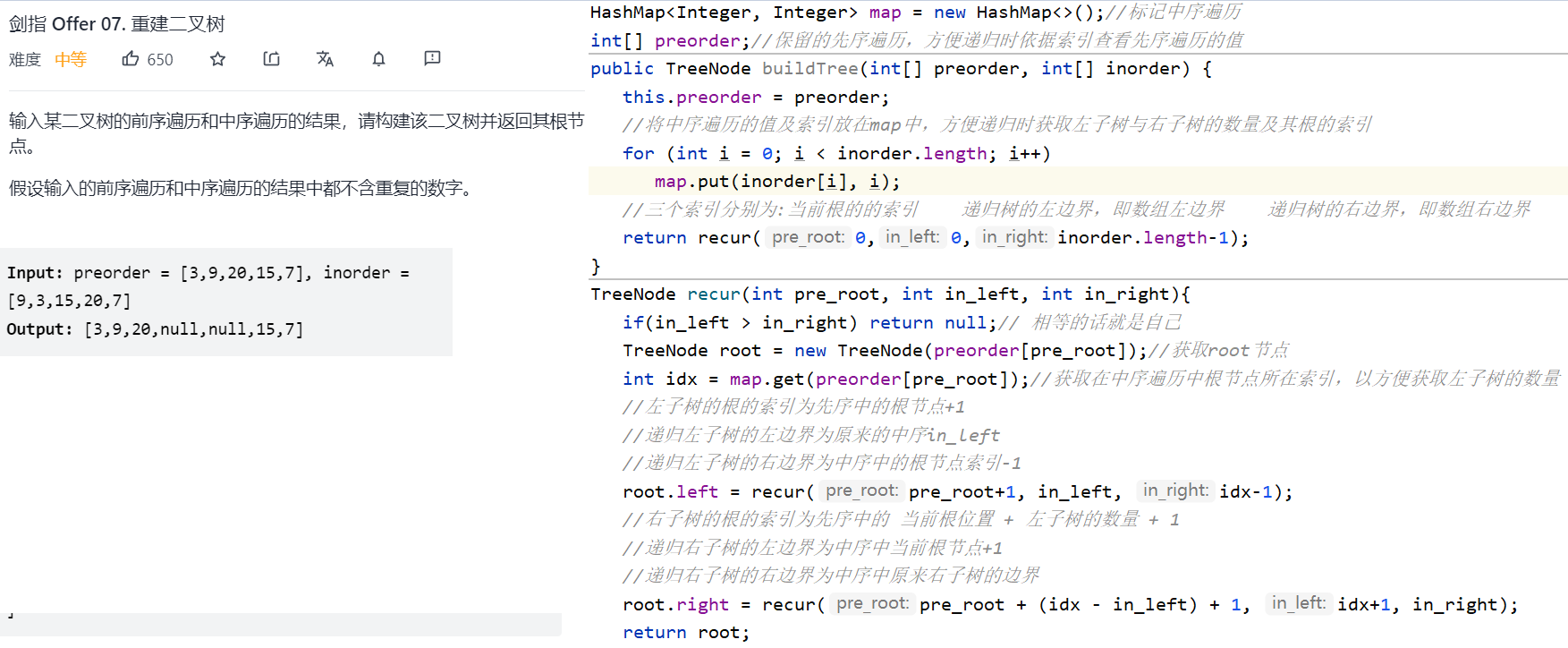

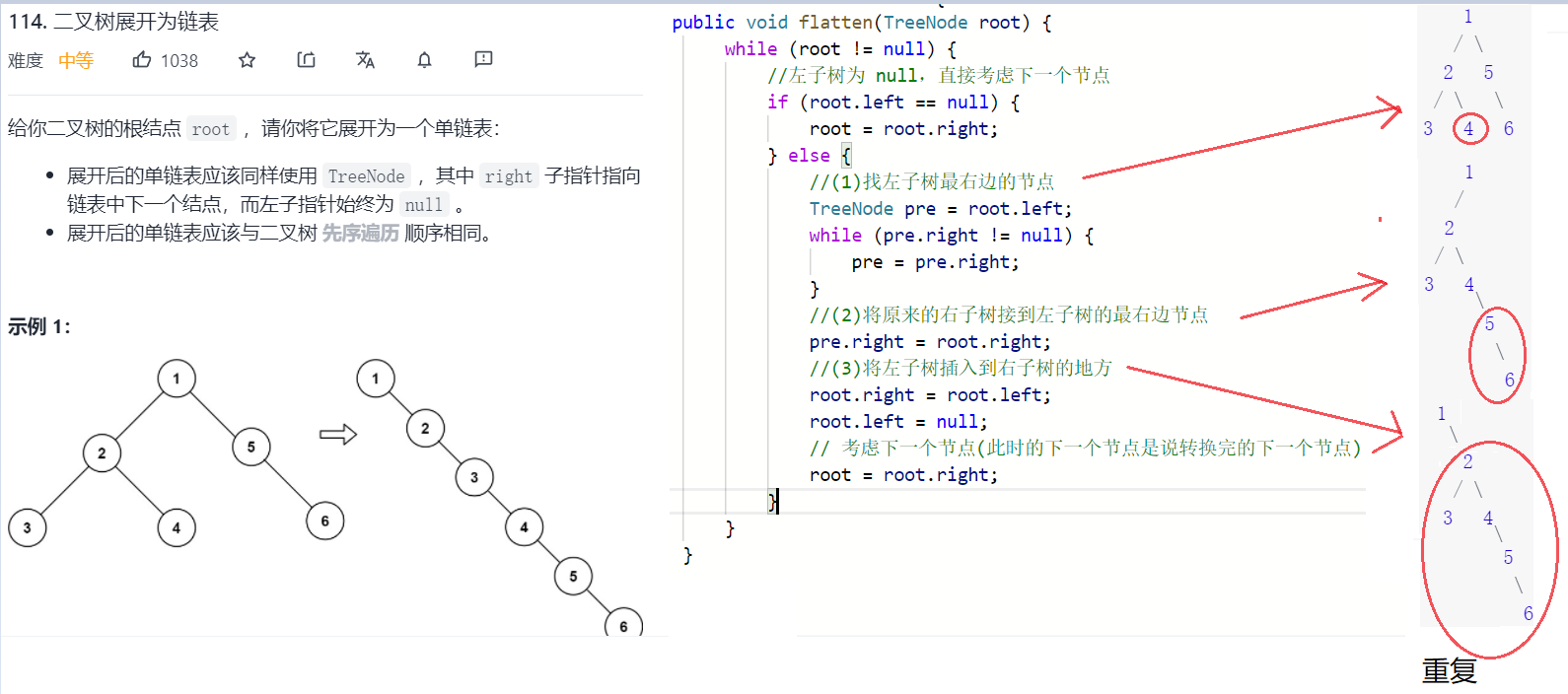
四.二叉树转换成链表

其他方法：前序遍历(链表与前序遍历相同)

该方法叫做：寻找前驱节点

五.二叉搜索树

二叉搜索树（Binary Search Tree, BST）是一种特殊的二叉树：对于每个父节点，其左子节点 的值小于等于父结点的值，其右子节点的值大于等于父结点的值。

二叉搜索树的中序遍历是递增序列(基础版)

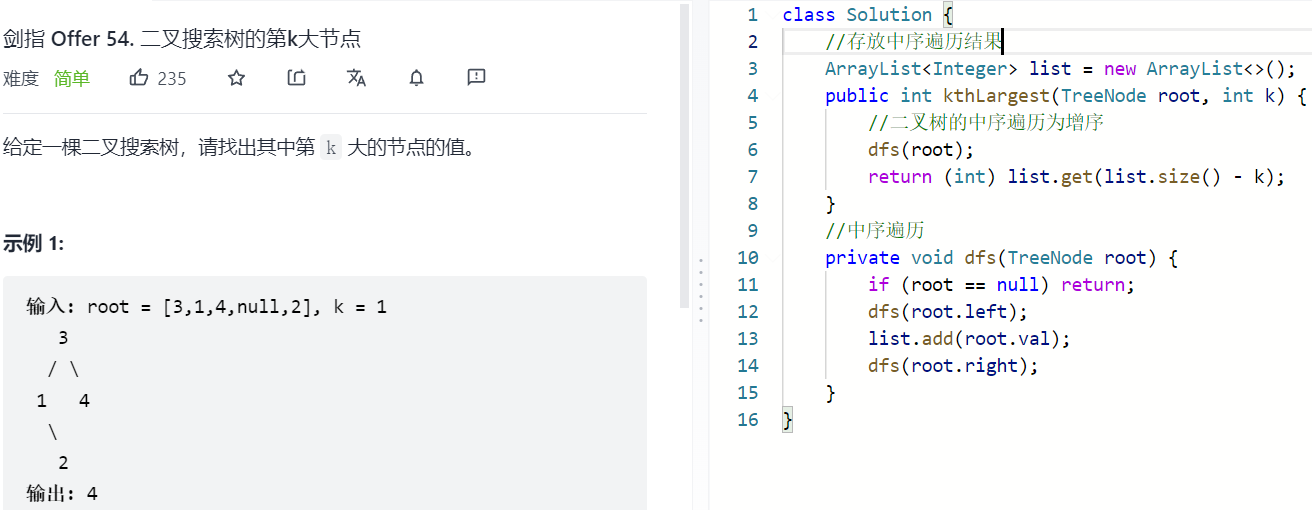
二叉搜索树的中序遍历是递增序列(升级版)

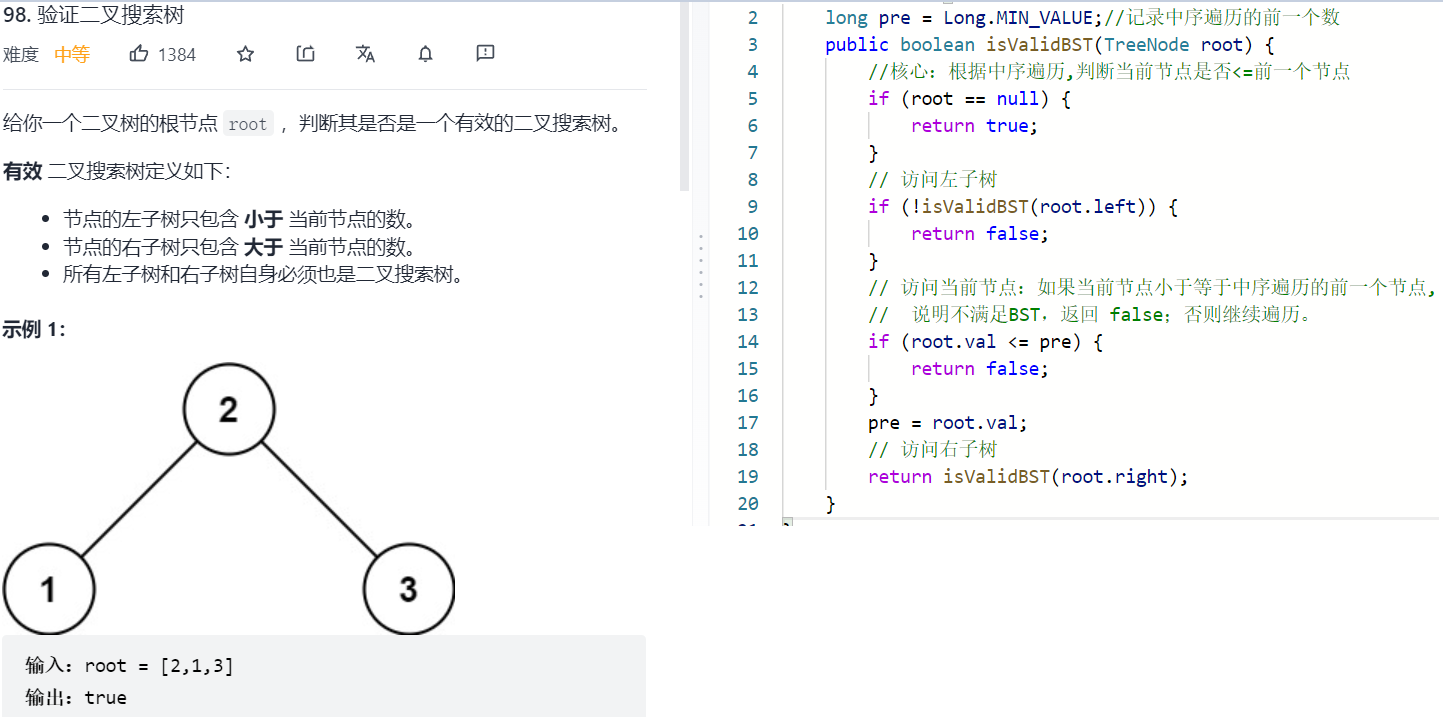
与普通二叉树不同的是，可以确定在哪个子树，不需要分别递归左右子树。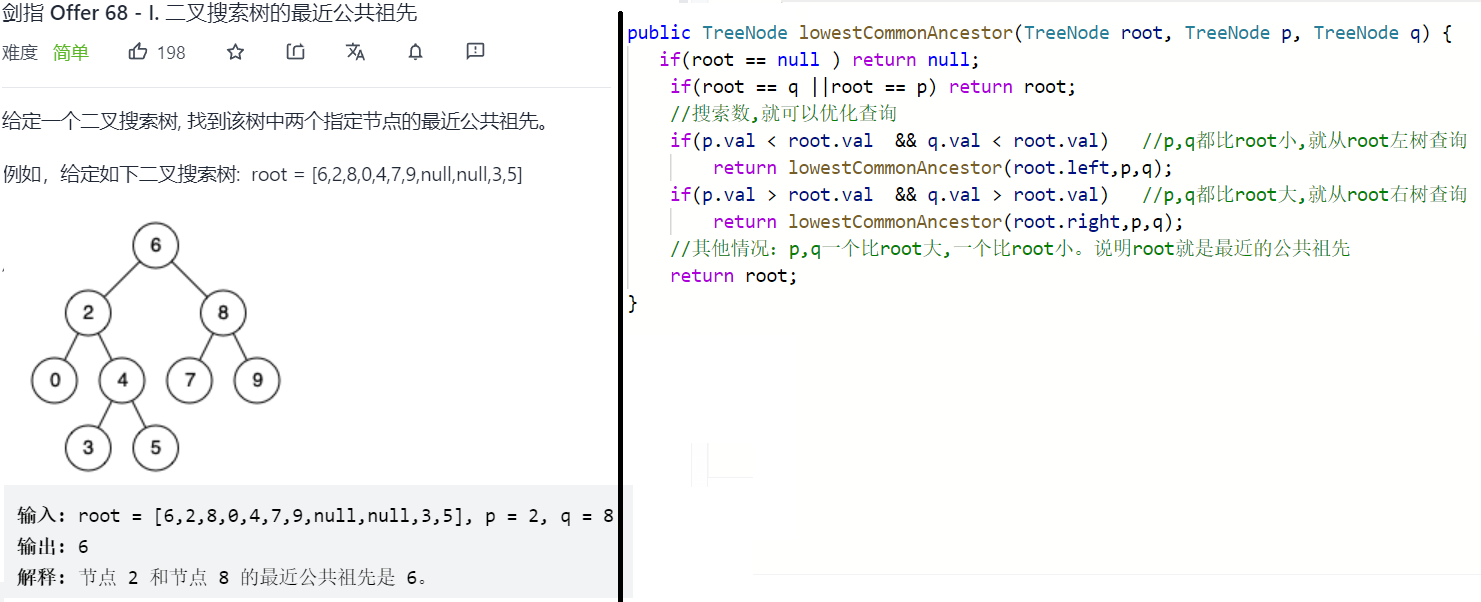

 核心：二叉搜索树的后序遍历满足：[小于根；大于根；根]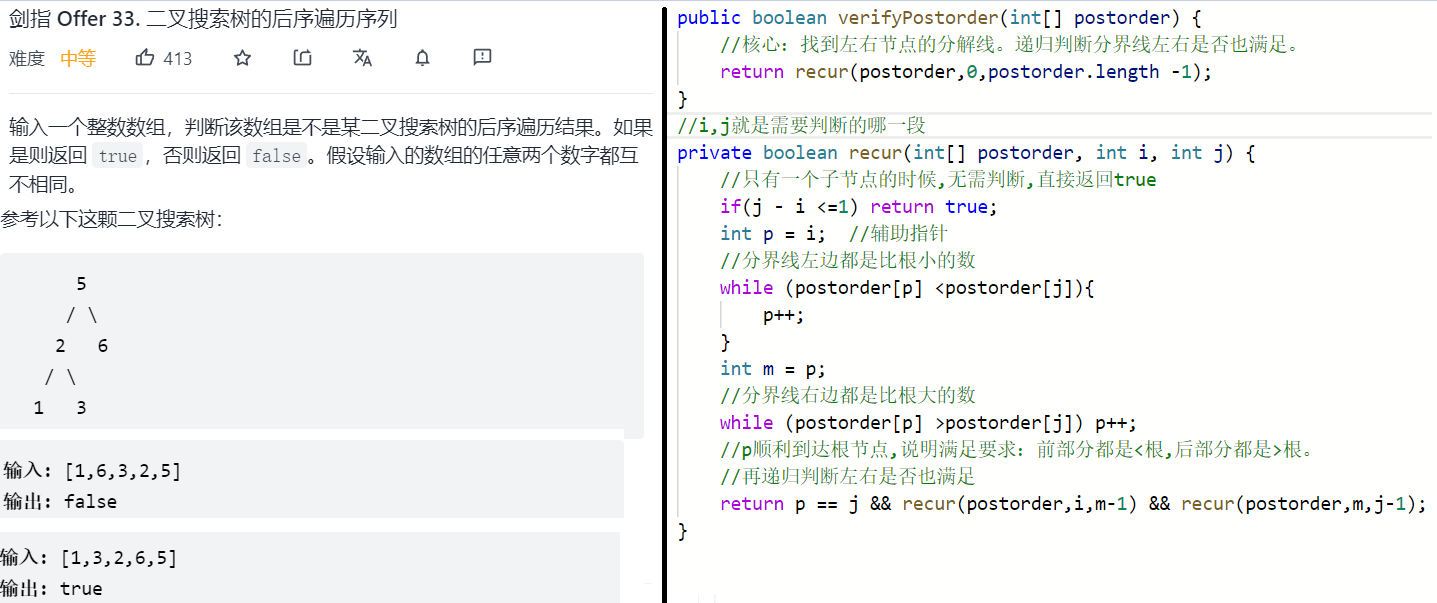　

 六.其他的树结构

累加树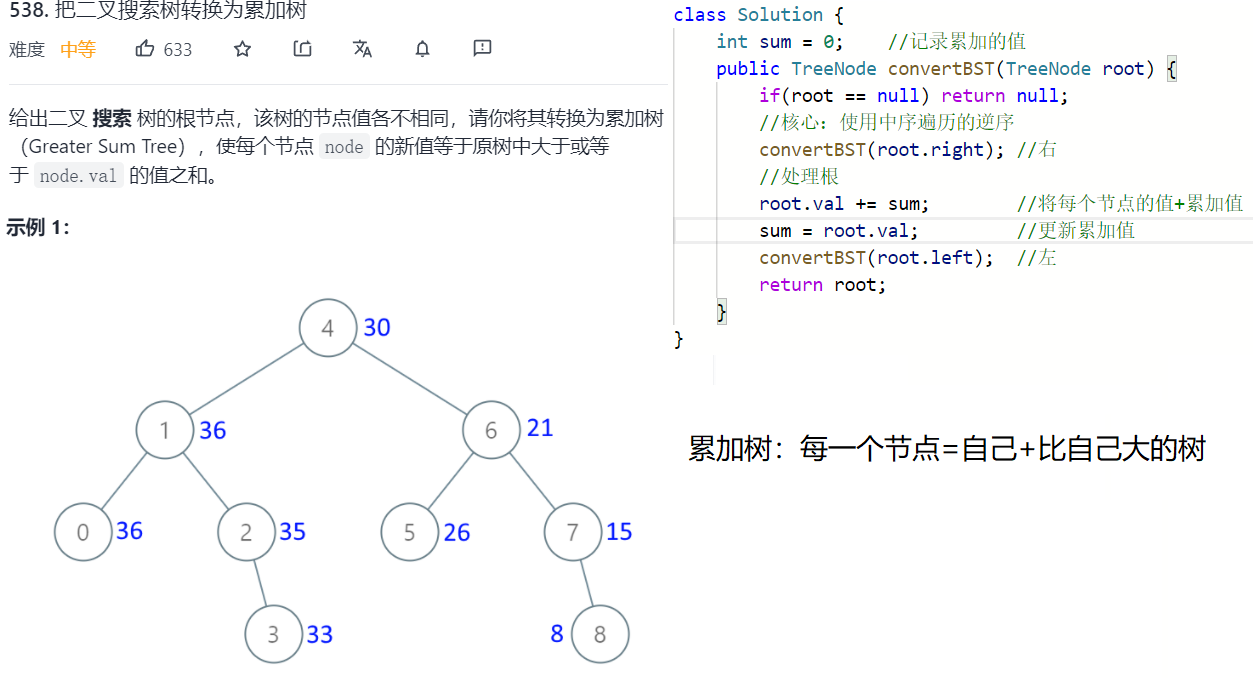

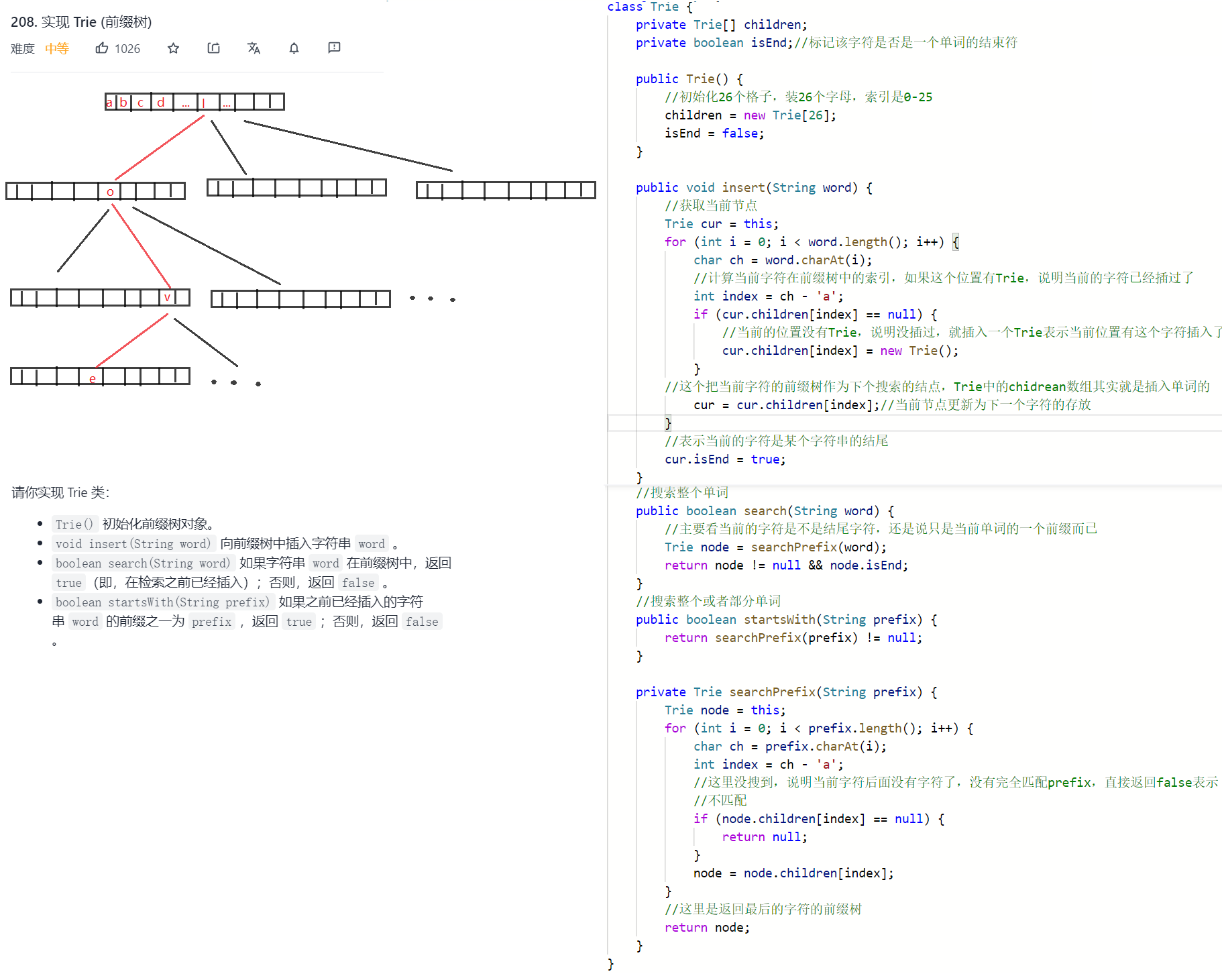
前缀树(字典树)：前缀树就是为了存放单词，可以用在一些单词补齐的功能上。

 寄语：就算是咸鱼，你也不是最咸的那条