LeetCode-134-加油站

134. 加油站

难度中等662收藏分享切换为英文接收动态反馈

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

• 如果题目有解，该答案即为唯一答案。
• 输入数组均为非空数组，且长度相同。
• 输入数组中的元素均为非负数。

示例 1:

输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: 
gas  = [2,3,4]
cost = [3,4,3]

输出: -1

解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

image-20210615091339545

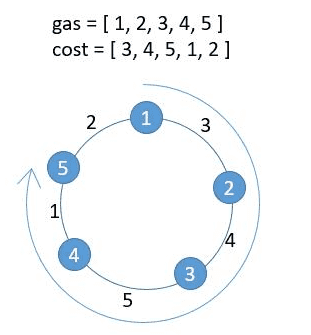
每个节点表示添加的油量，每条边表示消耗的油量。题目的意思就是问我们从哪个节点出发，还可以回到该节点。只能顺时针方向走。

下图的黑色折线图即总油量剩余值，若要满足题目的要求：跑完全程再回到起点，总油量剩余值的任意部分都需要在X轴以上，且跑到终点时：总剩余汽油量 >= 0。

为了让黑色折线图任意部分都在 X 轴以上，我们需要向上移动黑色折线图，直到所有点都在X轴或X轴以上。此时，处在X轴的点即为出发点。即黑色折线图的最低值的位置：index = 3。

image-20210615094708548

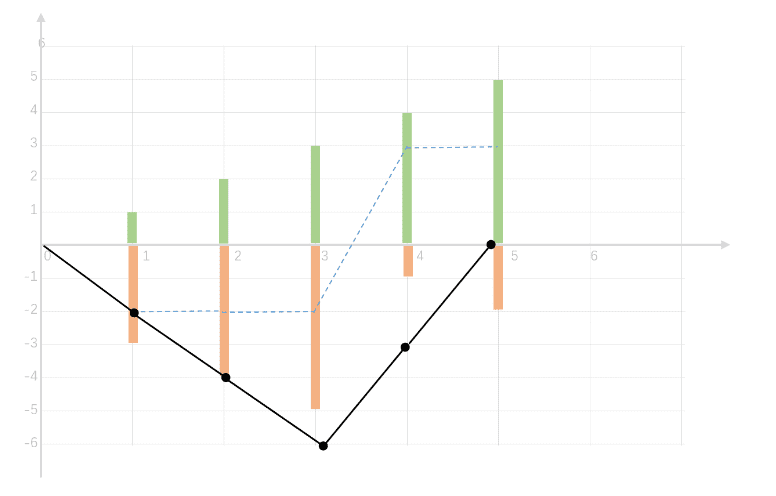
柱状图
绿色：可添加的汽油 gas[i]
橙色：消耗的汽油 cose[i]

折线图：
虚线（蓝色）：当前加油站的可用值
实线（黑色）：从0开始的总剩余汽油量

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int len = gas.length;
        int spare = 0;
        int minSpare = Integer.MAX_VALUE;
        int minIndex = 0;

        for (int i = 0; i < len; i++) {
            spare += gas[i] - cost[i];
            if (spare < minSpare) {
                minSpare = spare;
                minIndex = i;
            }
        }

        return spare < 0 ? -1 : (minIndex + 1) % len;
    }

}

image-20210615094755024

返回了所有节点是不是良好出发点

image-20210615100440984

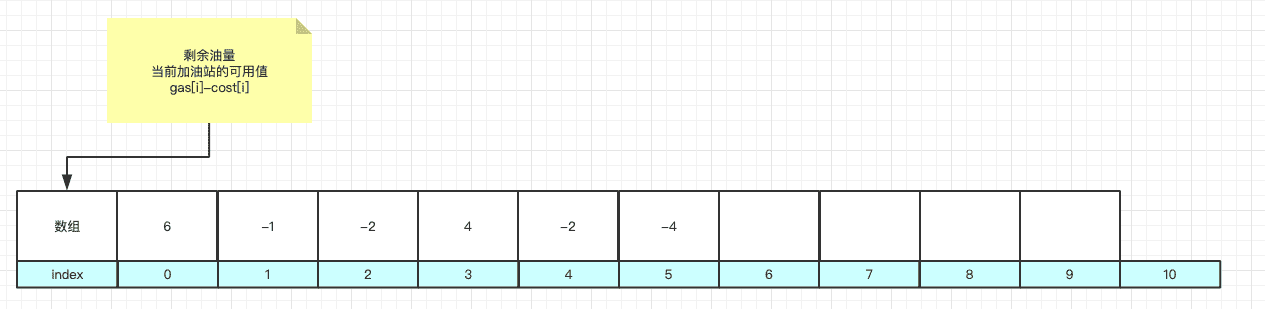
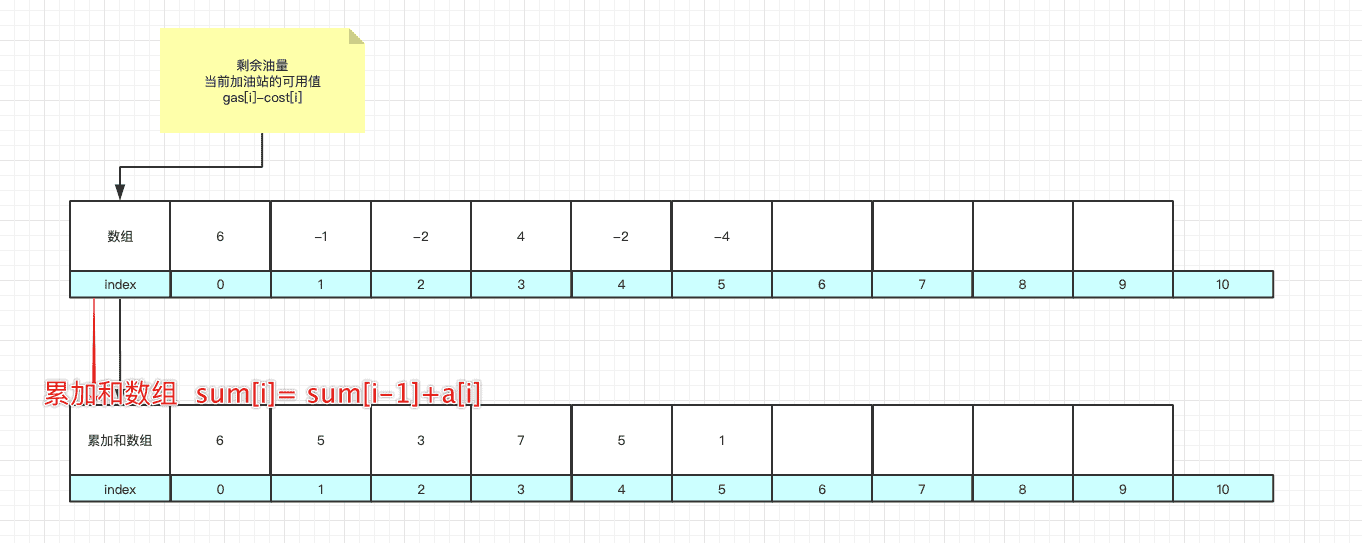
• 累加和数组

image-20210615100649462

image-20210615101009502

image-20210615101932718

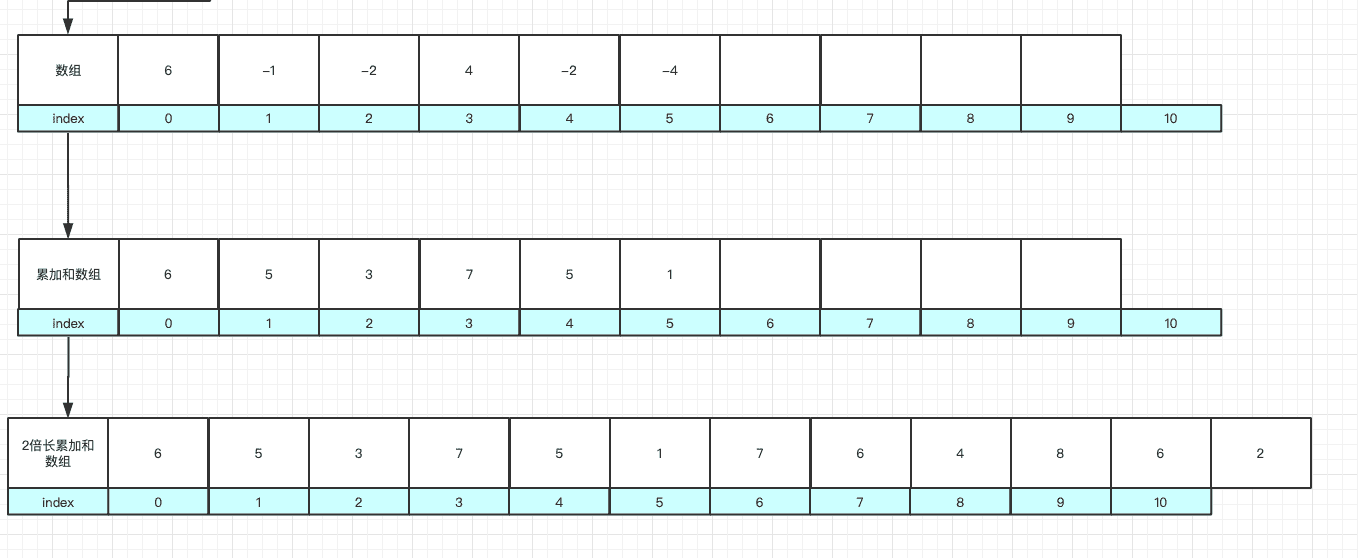
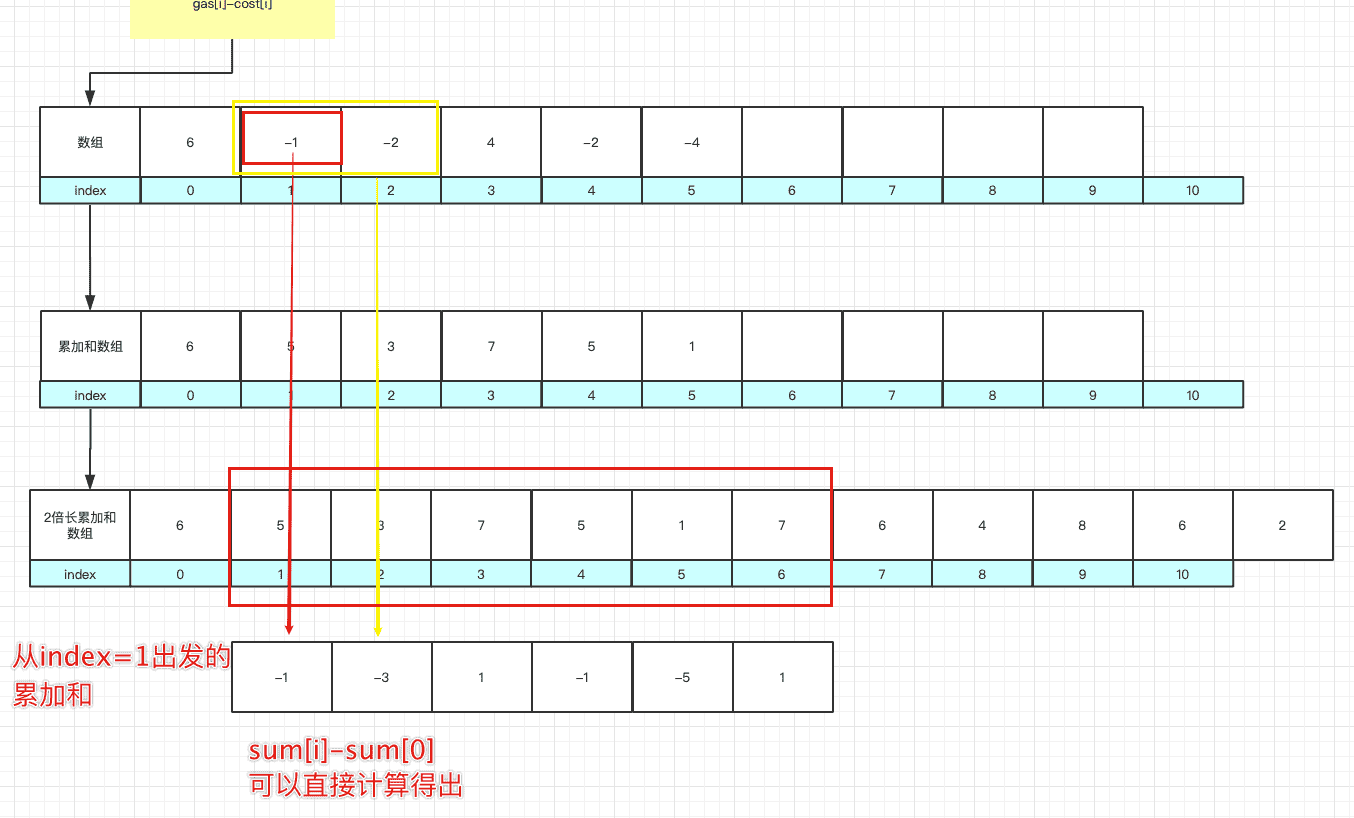
public static int canCompleteCircuit(int[] gas, int[] cost) {
   boolean[] good = goodArray(gas, cost);
   for (int i = 0; i < gas.length; i++) {
      if (good[i]) {
         return i;
      }
   }
   return -1;
}

public static boolean[] goodArray(int[] g, int[] c) {
   int N = g.length;
   int M = N << 1;//2 倍数组的长度
   int[] arr = new int[M];//2 倍数组
   for (int i = 0; i < N; i++) {
      arr[i] = g[i] - c[i];
      arr[i + N] = g[i] - c[i];//剩余油量数组
   }
   for (int i = 1; i < M; i++) {
      arr[i] += arr[i - 1];//2倍数组累计和 sum[i] = sum[i-1]+a[i]
   }
   LinkedList<Integer> w = new LinkedList<>();//窗口-> 双端队列-->
   for (int i = 0; i < N; i++) {
      while (!w.isEmpty() && arr[w.peekLast()] >= arr[i]) {//大值尾部出队
         w.pollLast();
      }
      w.addLast(i);//双端队列,尾巴加入index
   }
   boolean[] ans = new boolean[N];
   for (int offset = 0, i = 0, j = N; j < M; offset = arr[i++], j++) {
      if (arr[w.peekFirst()] - offset >= 0) {
         ans[i] = true;
      }
      if (w.peekFirst() == i) {
         w.pollFirst();
      }
      while (!w.isEmpty() && arr[w.peekLast()] >= arr[j]) {
         w.pollLast();
      }
      w.addLast(j);
   }
   return ans;
}