LeetCode-69-x 的平方根

69. x 的平方根

难度简单

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

我这里采用迭代中常见的二分法。每次查看区间内的中间值，检验它是否符合标准。
举个例子，假如我们要找到 10 的平方根。我们需要先看 1 到 10 的中间数值，也就是 11/2=5.5。5.5 的平方是大于 10 的，所以我们要一个更小的数值，就看 5.5 和 1 之间的 3.25。由于 3.25 的平方也是大于 10 的，继续查看 3.25 和 1 之间的数值，也就是 2.125。这时，2.125 的平方小于 10 了，所以看 2.125 和 3.25 之间的值，一直继续下去，直到发现某个数的平方正好是10。

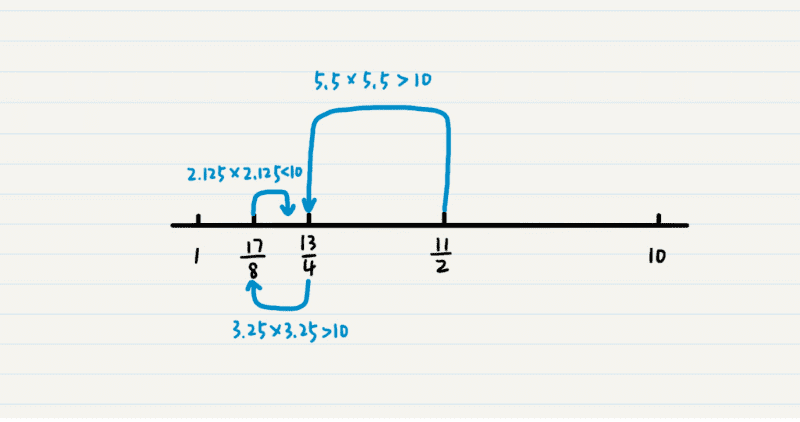
image-20210519095103661

class Solution {
    
    public static int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        if (x < 3) {
            return 1;
        }
        long ans = 1;
        long L = 1;
        long R = x;
        long M = 0;
        while (L <= R) {
            M = (L + R) / 2;
            if (M * M <= x) {
                ans = M;
                L = M + 1;
            } else {
                R = M - 1;
            }
        }
        return (int) ans;
    }

}

image-20210519095258766

class Solution {
    public int mySqrt(int x) {
        int left = 0,right = x;
        int ans = -1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if((long)mid * mid <= x){
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }
}

image-20210519095410204