文章目录
- 一、生成函数应用场景
- 二、使用生成函数求解递推方程
参考博客 :
- 【组合数学】生成函数 简要介绍 ( 生成函数定义 | 牛顿二项式系数 | 常用的生成函数 | 与常数相关 | 与二项式系数相关 | 与多项式系数相关 )
- 【组合数学】生成函数 ( 线性性质 | 乘积性质 )
- 【组合数学】生成函数 ( 移位性质 )
- 【组合数学】生成函数 ( 求和性质 )
- 【组合数学】生成函数 ( 换元性质 | 求导性质 | 积分性质 )
- 【组合数学】生成函数 ( 性质总结 | 重要的生成函数 ) ★
- 【组合数学】生成函数 ( 生成函数示例 | 给定通项公式求生成函数 | 给定生成函数求通项公式 )
一、生成函数应用场景
生成函数应用场景 :
- 求解递推方程
- 多重集
r
r
r 组合计数 - 不定方程解个数
- 整数拆分
多重集
r
r
r 组合计数 , 之前 只能计数特殊情况下的组合数 , 也就是选取数
r
r
r 小于多重集每一项的重复度 , 才有 组合数
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r) , 如果
r
r
r 大于重复度 , 就需要使用生成函数进行求解 ;
不定方程的解个数 , 之前只能求解 没有约束的情况 , 如果对变量有约束 , 如
x
1
x_1
x1 只能在某个区间取值 , 这种情况下 , 就必须使用生成函数进行求解 ;
整数拆分 , 将一个正数拆分多若干整数之和 , 拆分方案个数 , 也可以通过生成函数进行计算 ;
回顾多重集排列组合 :
- 可重复的元素 , 有序的选取 , 对应 多重集的排列 ;
全
排
列
=
n
!
n
1
!
n
2
!
⋯
n
k
!
全排列 = \cfrac{n!}{n_1! n_2! \cdots n_k!}
全排列=n1!n2!⋯nk!n! , 非全排列k
r
,
r
≤
n
i
k^r , \ \ r\leq n_i
kr, r≤ni - 可重复的元素 , 无序的选取 , 对应 多重集的组合 ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
二、使用生成函数求解递推方程
递推方程 :
a
n
−
5
a
n
−
1
+
6
a
n
−
2
=
0
a_n - 5a_{n-1} + 6a_{n-2} = 0
an−5an−1+6an−2=0
初值 :
a
0
=
1
,
a
1
=
2
a_0 = 1, a_1 = 2
a0=1,a1=2
{
a
n
}
\{a_n\}
{an} 数列为
{
a
0
,
a
1
,
a
2
,
a
3
,
⋯
,
a
n
,
⋯
}
\{ a_0 , a_1, a_2, a_3 , \cdots , a_n , \cdots\}
{a0,a1,a2,a3,⋯,an,⋯}
a
n
a_n
an对应的生成函数是
G
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
G(x) = a_0 + a_1 x + a_2 x^2 + a_3x^3 + \cdots
G(x)=a0+a1x+a2x2+a3x3+⋯
根据递推方程 , 同时为了使得后面的项可以约掉 , 使用
−
5
x
-5x
−5x 乘以
G
(
x
)
G(x)
G(x) 生成函数 , 使用
+
6
x
2
+6x^2
+6x2 乘以
G
(
x
)
G(x)
G(x) , 得到如下三个式子 ,
−
5
x
-5x
−5x 乘以
G
(
x
)
G(x)
G(x) 得到的第一项就是
x
x
x 的一次方项 , 将该项对应到
G
(
x
)
G(x)
G(x) 中的
x
x
x 一次方项下面 ,
+
6
x
2
+6x^2
+6x2 乘以
G
(
x
)
G(x)
G(x) 得到的第一项就是
x
x
x 的二次方项 , 将该项对应到
G
(
x
)
G(x)
G(x) 中的
x
x
x 二次方项下面 ;
G
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ G(x) = a_0 + a_1 x + a_2 x^2 + a_3x^3 + \cdots
G(x)=a0+a1x+a2x2+a3x3+⋯
−
5
x
G
(
x
)
=
−
5
a
0
x
−
5
a
1
x
2
−
5
a
2
x
3
−
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -5x \ G(x) = \ \ \ \ -5a_0x - 5a_1x^2 - 5a_2x^3 - \cdots
−5x G(x)= −5a0x−5a1x2−5a2x3−⋯
6
x
2
G
(
x
)
=
+
6
a
0
x
2
+
6
a
x
3
+
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 6x^2 \,G(x) = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \,6a_0x^2 + 6a_x^3 + \cdots
6x2G(x)= +6a0x2+6ax3+⋯
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
a
0
+
(
a
1
−
5
a
0
)
x
(1-5x+6x^2)G(x) =a_0 + (a_1 - 5a_0)x
(1−5x+6x2)G(x)=a0+(a1−5a0)x
上述横线下的式子是 横线上面 三个式子相加的结果 ;
观察上述右侧 第三列 , 图中红框部分 ;
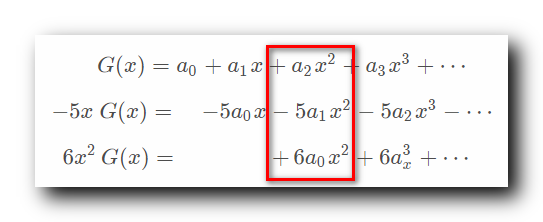
上述幂次对齐后 , 出现的等号右侧的第三列
+
a
2
x
2
−
5
a
1
x
2
+
6
a
0
x
2
+ a_2 x^2 -5a_1x^2 + \,6a_0x^2
+a2x2−5a1x2+6a0x2 , 将其中
x
2
x^2
x2 提取出来得到
(
a
2
−
5
a
1
+
6
a
0
)
x
2
(a_2 - 5a_1 + 6a_0)x^2
(a2−5a1+6a0)x2 , 正好对应递推方程
a
n
−
5
a
n
−
1
+
6
a
n
−
2
=
0
a_n - 5a_{n-1} + 6a_{n-2} = 0
an−5an−1+6an−2=0 ,
因此有
a
2
−
5
a
1
+
6
a
0
=
0
a_2 - 5a_1 + 6a_0 = 0
a2−5a1+6a0=0 , 进而可以得到
(
a
2
−
5
a
1
+
6
a
0
)
x
2
=
0
(a_2 - 5a_1 + 6a_0)x^2 = 0
(a2−5a1+6a0)x2=0
由此可以看出 , 如果三个式子全部相加 , 下图 右侧蓝色矩形框内 , 全部都是
0
0
0 ;

目前右侧只剩下
a
0
+
a
1
x
−
5
a
0
x
a_0 + a_1x -5a_0x
a0+a1x−5a0x 三项 ; 其中的
a
0
=
1
,
a
1
=
−
2
a_0 = 1 , a_1 = -2
a0=1,a1=−2 是初值 ;
最终等式右侧是 :
1
−
2
x
−
5
x
=
1
−
7
x
1 - 2x - 5x = 1-7x
1−2x−5x=1−7x
将上述式子代入到
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
a
0
+
(
a
1
−
5
a
0
)
x
(1-5x+6x^2)G(x) =a_0 + (a_1 - 5a_0)x
(1−5x+6x2)G(x)=a0+(a1−5a0)x 中 , 使用
1
−
2
x
−
5
x
=
1
−
7
x
1 - 2x - 5x = 1-7x
1−2x−5x=1−7x 替换等式右侧的式子 , 得到 :
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
1
−
7
x
(1-5x+6x^2)G(x) =1-7x
(1−5x+6x2)G(x)=1−7x
G
(
x
)
=
1
−
7
x
1
−
5
x
+
6
x
2
G(x) = \cfrac{1-7x}{1-5x+6x^2}
G(x)=1−5x+6x21−7x
使用 给定 生成函数 , 求对应的级数 的 方法 , 将上述式子展开 , 参考 【组合数学】生成函数 ( 生成函数示例 | 给定通项公式求生成函数 | 给定生成函数求通项公式 ) 二、给定生成函数求级数 方法 ,
先将分母进行因式分解 , 然后设置两个待定系数 , 通分后 , 根据
x
x
x 项系数写出方程组 , 最终解该方程组 , 最终可以得到 :
G
(
x
)
=
1
−
7
x
1
−
5
x
+
6
x
2
=
5
1
−
2
x
−
4
1
−
3
x
G(x) = \cfrac{1-7x}{1-5x+6x^2} = \cfrac{5}{1-2x} - \cfrac{4}{1-3x}
G(x)=1−5x+6x21−7x=1−2x5−1−3x4
5
1
−
2
x
\cfrac{5}{1-2x}
1−2x5 对应的级数是 :
∑
n
=
0
∞
5
(
2
x
)
n
=
5
∑
n
=
0
∞
2
n
x
n
\sum\limits_{n=0}^\infty 5 (2x)^n = 5\sum\limits_{n=0}^\infty 2^n x^n
n=0∑∞5(2x)n=5n=0∑∞2nxn
4
1
−
3
x
\cfrac{4}{1-3x}
1−3x4 对应的级数是 :
∑
n
=
0
∞
(
−
4
)
(
3
x
)
n
=
−
4
∑
n
=
0
∞
3
n
x
n
\sum\limits_{n=0}^\infty (-4) (3x)^n = -4\sum\limits_{n=0}^\infty 3^n x^n
n=0∑∞(−4)(3x)n=−4n=0∑∞3nxn
最终生成函数的级数形式为 :
G
(
x
)
=
5
∑
n
=
0
∞
2
n
x
n
−
4
∑
n
=
0
∞
3
n
x
n
G(x) = 5\sum\limits_{n=0}^\infty 2^n x^n - 4\sum\limits_{n=0}^\infty 3^n x^n
G(x)=5n=0∑∞2nxn−4n=0∑∞3nxn
递推方程的通解 :
a
n
=
5
⋅
2
n
−
4
⋅
3
n
a_n = 5 \cdot 2^n - 4 \cdot 3^n
an=5⋅2n−4⋅3n
基本思路 : 有原来的递推方程 , 导出关于生成函数的递推方程 ;
 IDEA激活码
IDEA激活码


