文章目录
- 一、偏序关系
- 二、偏序集
- 三、可比
- 四、严格小于
- 五、覆盖
- 六、哈斯图
- 七、全序关系 ( 线序关系 )
- 八、拟序关系
- 九、拟序关系相关定理
- 十、偏序关系八种特殊元素
- 十一、链
- 十二、反链
- 十三、链与反链定理
参考博客 :
- 【集合论】序关系 ( 偏序关系 | 偏序集 | 偏序集示例 )
- 【集合论】序关系 ( 偏序集元素之间的关系 | 可比 | 严格小于 | 覆盖 | 哈斯图 )
- 【集合论】序关系 ( 哈斯图示例 | 整除关系哈斯图 | 包含关系哈斯图 | 加细关系哈斯图 )
- 【集合论】序关系 ( 全序关系 | 全序集 | 全序关系示例 | 拟序关系 | 拟序关系定理 | 三歧性 | 拟线序关系 | 拟线序集 )
- 【集合论】序关系 ( 偏序关系中八种特殊元素 | ① 最大元 | ② 最小元 | ③ 极大元 | ④ 极小元 | ⑤ 上界 | ⑥ 下界 | ⑦ 最小上界 上确界 | ⑧ 最小下界 下确界 )
- 【集合论】序关系 ( 链 | 反链 | 链与反链示例 | 链与反链定理 | 链与反链推论 | 良序关系 )
一、偏序关系
偏序关系 :
给定非空集合
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
R
R
R 关系是
A
A
A 集合上的二元关系 ,
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A ,
如果
R
R
R 关系满足以下性质 :
- 自反 : 关系图中所有顶点 都有环 ;
- 反对称 : 两个顶点之间 有
0
0
0 个或1
1
1 个有向边 ; - 传递 : 前提
a
→
b
,
b
→
c
a \to b , b\to c
a→b,b→c 不成立 默认传递 ; 前提a
→
b
,
b
→
c
a \to b , b\to c
a→b,b→c 成立 必须满足a
→
c
a \to c
a→c 存在 ;
则称
R
R
R 关系是
A
A
A 集合上的 偏序关系 ;
偏序关系表示 : 使用
≼
\preccurlyeq
≼ 符号表示偏序关系 , 读作 “小于等于” ;
符号化表示 :
<
x
,
y
>
∈
R
⇔
x
R
y
⇔
x
≼
y
<x,y> \in R \Leftrightarrow xRy \Leftrightarrow x \preccurlyeq y
<x,y>∈R⇔xRy⇔x≼y , 解读 :
<
x
,
y
>
<x,y>
<x,y> 有序对在偏序关系
R
R
R 中 , 则
x
x
x 与
y
y
y 之间有
R
R
R 关系 ,
x
x
x 小于等于
y
y
y ;
等价关系 是用于 分类 的 , 偏序关系 是用于 组织 的 , 在每个类的内部 , 赋予一个结构 ;
参考博客 : 【集合论】序关系 ( 偏序关系 | 偏序集 | 偏序集示例 )
二、偏序集
偏序集 :
≼
\preccurlyeq
≼ 关系 是
A
A
A 集合上的偏序关系 , 则称 集合
A
A
A 与 偏序关系
≼
\preccurlyeq
≼ 构成的 有序对
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 称为偏序集 ;
如果集合上有偏序关系 , 那么这个集合就称为偏序集 ;
参考博客 : 【集合论】序关系 ( 偏序关系 | 偏序集 | 偏序集示例 )
三、可比
可比 :
A
A
A 集合 , 该集合上存在 偏序关系
≼
\preccurlyeq
≼ 小于等于 ,
偏序集 是 集合 和 偏序关系 组成的有序对
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
要么是
x
≼
y
x \preccurlyeq y
x≼y , 要么就是
y
≼
x
y \preccurlyeq x
y≼x , 符号化表示是
x
≼
y
∨
y
≼
x
x \preccurlyeq y \lor y \preccurlyeq x
x≼y∨y≼x , 两种情况必选其一 ,
则称
x
x
x 与
y
y
y 是可比的 ;
只要
x
,
y
x, y
x,y 之间 存在偏序关系 , 不管谁在前 , 谁在后 , 都 统一称
x
x
x 与
y
y
y 是可比的 ;
参考博客 : 【集合论】序关系 ( 偏序集元素之间的关系 | 可比 | 严格小于 | 覆盖 | 哈斯图 )
四、严格小于
严格小于 概念需要基于 可比概念
严格小于 :
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
如果
x
,
y
x , y
x,y 是可比的 (
x
,
y
x,y
x,y 之间存在偏序关系 ) , 但是
x
x
x 与
y
y
y 不相等 , 则称
x
x
x 严格小于
y
y
y ;
符号化表示 :
x
≼
y
∧
x
≠
y
⇔
x
≺
y
x \preccurlyeq y \land x \not= y \Leftrightarrow x \prec y
x≼y∧x=y⇔x≺y
参考博客 : 【集合论】序关系 ( 偏序集元素之间的关系 | 可比 | 严格小于 | 覆盖 | 哈斯图 )
五、覆盖
覆盖 概念需要基于 严格小于概念
覆盖 :
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
,
z
x, y , z
x,y,z 是
A
A
A 集合中的元素 ,
x
,
y
,
z
∈
A
x , y , z \in A
x,y,z∈A ,
x
x
x 严格小于
y
y
y ,
x
≺
y
x \prec y
x≺y ,
不存在
z
z
z , 使
x
x
x 严格小于
z
z
z , 并且
z
z
z 严格小于
y
y
y ,
则称
y
y
y 覆盖
x
x
x ; ( 注意是 大 覆盖 小 )
偏序关系中 大 覆盖 小
符号化表示 :
x
≺
y
∧
¬
∃
z
(
z
∈
A
∧
x
≺
y
≺
z
)
x \prec y \land \lnot \exist z( z \in A \land x \prec y \prec z )
x≺y∧¬∃z(z∈A∧x≺y≺z)
参考博客 : 【集合论】序关系 ( 偏序集元素之间的关系 | 可比 | 严格小于 | 覆盖 | 哈斯图 )
六、哈斯图
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
哈斯图 :
① 顶点 : 使用 顶点 表示
A
A
A 集合中的元素 ;
② 无向边 : 当且仅当
y
y
y 覆盖
x
x
x 时 ,
y
y
y 顶点在
x
x
x 顶点 上方 , 并且在
x
x
x 顶点 与
y
y
y 顶点之间 绘制一条 无向边 ;
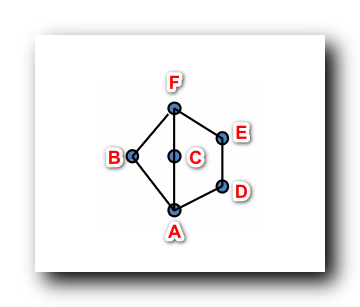
上图是
6
6
6 元集 上的偏序关系
≼
\preccurlyeq
≼
A
A
A 元素比
B
,
C
,
D
B,C,D
B,C,D 元素都小
偏序关系是传递的 ,
A
A
A 比
B
B
B 小 ,
B
B
B 比
F
F
F 小 , 因此
A
A
A 比
F
F
F 小
最下面的元素
A
A
A 是最小的 , 所有的元素都比
A
A
A 大 ( 包括
A
A
A , 偏序关系是自反的 )
最上面的元素
F
F
F 是最大的 , 所有的元素都比
F
F
F 小 ( 包括
F
F
F , 偏序关系是自反的 )
B
C
D
E
BCDE
BCDE 四个元素互相都不可比
哈斯图 与 关系图对比 省略的内容 :
① 环 : 偏序关系是自反的 , 因此 每个顶点上都有环 , 可以省略掉环
② 箭头 : 偏序关系是反对称的 , 因此 两个顶点两两之间肯定没有双向边 , 都是单向边 , 因此可以省略箭头方向
③ 默认方向 : 使用上下位置表示箭头的方向 , 箭头默认向上 , 偏序是 小于等于 , 最小的在最小面, 最大的在最上面 ;
参考博客 :
- 【集合论】序关系 ( 偏序集元素之间的关系 | 可比 | 严格小于 | 覆盖 | 哈斯图 )
- 【集合论】序关系 ( 哈斯图示例 | 整除关系哈斯图 | 包含关系哈斯图 | 加细关系哈斯图 )
七、全序关系 ( 线序关系 )
A
A
A 集合与该集合之上的 偏序关系
≼
\preccurlyeq
≼ 组成的有序对是 :
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 偏序集 ;
A
A
A 集合中 任意元素
x
,
y
x, y
x,y 都 可比 ;
则称
≼
\preccurlyeq
≼ 关系是
A
A
A 集合上的 全序关系, 又称为 线序关系 ;
称
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 为全序集 ( 线序集 ) ;
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 偏序集 是全序集
当且仅当
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 偏序集的哈斯图是一条直线
参考博客 : 【集合论】序关系 ( 全序关系 | 全序集 | 全序关系示例 | 拟序关系 | 拟序关系定理 | 三歧性 | 拟线序关系 | 拟线序集 )
八、拟序关系
非空集合
A
A
A , 二元关系
R
R
R 是
A
A
A 集合上的二元关系 ;
符号化表示 :
A
≠
∅
A \not= \varnothing
A=∅ ,
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A ;
如果 二元关系
R
R
R 是 反自反 , 传递 的 ,
则称
R
R
R 关系是
A
A
A 集合上的拟序关系 ,
使用
≺
\prec
≺ 表示拟序关系 ,
称
<
A
,
≺
>
<A , \prec>
<A,≺> 是拟序集 ;
偏序关系
≼
\preccurlyeq
≼ 是 小于等于 关系 , 拟序关系
≺
\prec
≺ 就是 严格小于 关系 ;
拟序关系示例 : 大于 , 小于 , 真包含 , 都是拟序关系 ;
拟序关系 完整的性质是 反自反 , 反对称 , 传递 ,
之所以概念中没有提 反对称 性质 , 是因为 根据 反自反 , 传递性质 , 可以推导出 反对称 性质 ;
数学中倾向于使用最小的条件进行定义 , 因此这里将反对称性去掉 ;
参考博客 : 【集合论】序关系 ( 全序关系 | 全序集 | 全序关系示例 | 拟序关系 | 拟序关系定理 | 三歧性 | 拟线序关系 | 拟线序集 )
九、拟序关系相关定理
定理 1 :
非空集合
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
≼
\preccurlyeq
≼ 是非空集合
A
A
A 上的偏序关系 ,
≺
\prec
≺ 是非空集合
A
A
A 上的拟序关系 ;
① 偏序关系性质 :
≼
\preccurlyeq
≼ 是 自反 , 反对称 , 传递的
② 拟序关系性质 :
≺
\prec
≺ 是 反自反 , 反对称 , 传递的
③ 偏序关系 -> 拟序关系 : 偏序关系 减去 恒等关系 就是 拟序关系 ,
≼
−
I
A
=
≺
\preccurlyeq - I_A = \prec
≼−IA=≺
④ 拟序关系 -> 偏序关系 : 拟序关系 与 恒等关系 的并集就是 偏序关系 ,
≺
∪
I
A
=
≼
\prec \cup I_A = \preccurlyeq
≺∪IA=≼ ;
定理 2 :
非空集合
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
≺
\prec
≺ 是非空集合
A
A
A 上的拟序关系 ;
①
x
≺
y
x \prec y
x≺y ,
x
=
y
x=y
x=y ,
y
≺
x
y \prec x
y≺x 中最多有一个成立 ;
使用反证法 , 任意两个成立都会导致
x
≺
x
x \prec x
x≺x ;
②
(
x
≺
y
∧
x
=
y
)
∧
(
y
≺
x
∧
x
=
y
)
⇒
x
=
y
(x\prec y \land x = y) \land (y \prec x \land x=y) \Rightarrow x = y
(x≺y∧x=y)∧(y≺x∧x=y)⇒x=y
定理 3 三歧性 , 拟线序 :
非空集合
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
≺
\prec
≺ 是非空集合
A
A
A 上的拟序关系 ;
如果
x
≺
y
x \prec y
x≺y ,
x
=
y
x=y
x=y ,
y
≺
x
y \prec x
y≺x 中仅有一个城里 , 那么称
≺
\prec
≺ 拟序关系 具有 三歧性 ;
有三歧性的 逆序关系
≺
\prec
≺ 称为
A
A
A 集合上的 拟线序关系 , 又称为拟全序关系 ;
<
A
≺
>
<A \prec>
<A≺> 被称为 拟线序集 ;
参考博客 : 【集合论】序关系 ( 全序关系 | 全序集 | 全序关系示例 | 拟序关系 | 拟序关系定理 | 三歧性 | 拟线序关系 | 拟线序集 )
十、偏序关系八种特殊元素
参考博客 : 【集合论】序关系 ( 偏序关系中八种特殊元素 | ① 最大元 | ② 最小元 | ③ 极大元 | ④ 极小元 | ⑤ 上界 | ⑥ 下界 | ⑦ 最小上界 上确界 | ⑧ 最小下界 下确界 )
十一、链
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
偏序集中一组元素组成集合
B
B
B , 如果
B
B
B 集合中的元素两两都可比 , 则称
B
B
B 集合是该偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 的链 ;
符号化表示 :
∀
x
∀
y
(
x
∈
B
∧
y
∈
B
→
x
与
y
可
比
)
\forall x \forall y ( x \in B \land y \in B \to x 与 y 可比 )
∀x∀y(x∈B∧y∈B→x与y可比)
链的本质是一个集合
∣
B
∣
|B|
∣B∣ 是链的长度
参考博客 :
- 【集合论】偏序关系 相关题目解析 ( 偏序关系 中的特殊元素 | 绘制哈斯图 | 链 | 反链 )
- 【集合论】序关系 ( 链 | 反链 | 链与反链示例 | 链与反链定理 | 链与反链推论 | 良序关系 )
十二、反链
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
偏序集中一组元素组成集合
B
B
B , 如果
B
B
B 集合中的元素两两都 不可比 , 则称
B
B
B 集合是该偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 的 反链 ;
符号化表示 :
∀
x
∀
y
(
x
∈
B
∧
y
∈
B
∧
x
≠
y
→
x
与
y
不
可
比
)
\forall x \forall y ( x \in B \land y \in B \land x\not= y \to x 与 y 不可比 )
∀x∀y(x∈B∧y∈B∧x=y→x与y不可比)
反链的本质是一个集合
∣
B
∣
|B|
∣B∣ 是反链的长度
参考博客 :
- 【集合论】偏序关系 相关题目解析 ( 偏序关系 中的特殊元素 | 绘制哈斯图 | 链 | 反链 )
- 【集合论】序关系 ( 链 | 反链 | 链与反链示例 | 链与反链定理 | 链与反链推论 | 良序关系 )
十三、链与反链定理
参考博客 :
- 【集合论】偏序关系 相关题目解析 ( 偏序关系 中的特殊元素 | 绘制哈斯图 | 链 | 反链 )
- 【集合论】序关系 ( 链 | 反链 | 链与反链示例 | 链与反链定理 | 链与反链推论 | 良序关系 )
 IDEA激活码
IDEA激活码


