递推方程求解 :

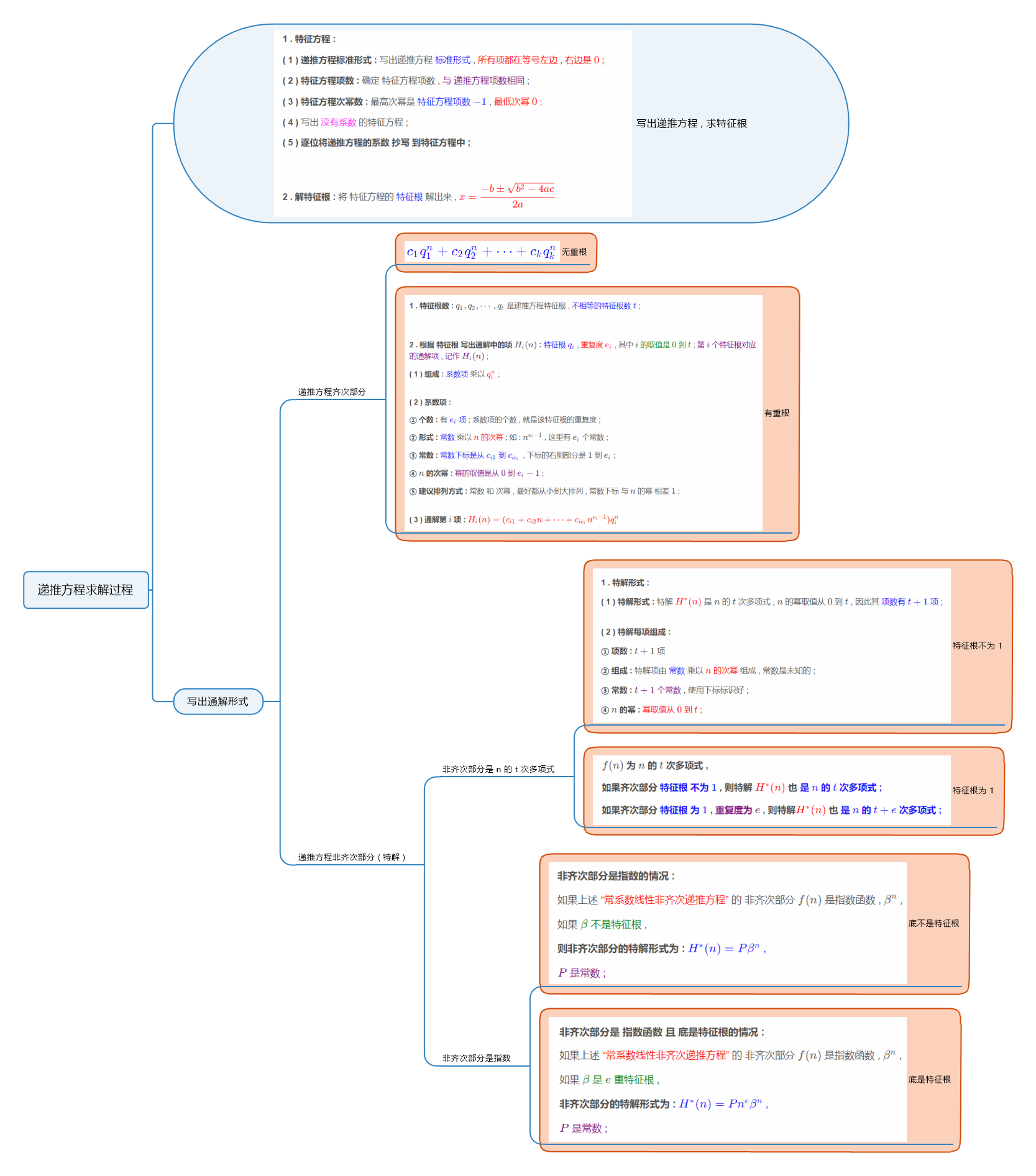
一、常系数线性齐次递推方程求解过程

---

常系数线性齐次递推方程求解过程 :

1 . 特征方程 :

( 1 ) 递推方程标准形式 : 写出递推方程 标准形式 , 所有项都在等号左边 , 右边是

0

0

0 ;

( 2 ) 特征方程项数 : 确定 特征方程项数 , 与 递推方程项数相同 ;

( 3 ) 特征方程次幂数 : 最高次幂是 特征方程项数

−

1

-1

−1 , 最低次幂

0

0

0 ;

( 4 ) 写出 没有系数 的特征方程 ;

( 5 ) 逐位将递推方程的系数 抄写 到特征方程中 ;

2 . 解特征根 : 将 特征方程的 特征根 解出来 ,

x

=

−

b

±

b

2

−

4

a

c

2

a

x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}

x=2a−b±b2−4ac
​​

3 . 构造递推方程的通解 :

( 1 ) 无重根 : 构造

c

1

q

1

n

+

c

2

q

2

n

+

⋯

+

c

k

q

k

n

c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n

c1​q1n​+c2​q2n​+⋯+ck​qkn​ 形式的线性组合 , 该线性组合就是递推方程的 通解 ;

( 2 ) 有重根 : 参考下面的 “有重根下的通解形式列出” 内容 ;

4 . 求通解中的常数 :

( 1 ) 代入初值获得方程组 : 将递推方程初值代入通解 , 得到

k

k

k 个

k

k

k 元方程组 , 通过 解该方程组 , 得到 通解中的常数 ;

( 2 ) 代入常数获得通解 : 将常数代入通解 , 就可以得到最终的递推方程的解 ;

递推方程 -> 特征方程 -> 特征根 -> 通解 -> 代入初值求通解常数

二、常系数线性齐次递推方程求解过程 ( 有重根下的通解形式 )

---

1 . 特征根数 :

q

1

,

q

2

,

⋯
 

,

q

t

q_1, q_2, \cdots , q_t

q1​,q2​,⋯,qt​ 是递推方程特征根 , 不相等的特征根数

t

t

t ;

2 . 根据 特征根 写出通解中的项

H

i

(

n

)

H_i(n)

Hi​(n) : 特征根

q

i

q_i

qi​ , 重复度

e

i

e_i

ei​ , 其中

i

i

i 的取值是

0

0

0 到

t

t

t ; 第

i

i

i 个特征根对应的通解项 , 记作

H

i

(

n

)

H_i(n)

Hi​(n) ;

( 1 ) 组成 : 系数项 乘以

q

i

n

q_i^n

qin​ ;

( 2 ) 系数项 :

① 个数 : 有

e

i

e_i

ei​ 项 ; 系数项的个数 , 就是该特征根的重复度 ;

② 形式 : 常数 乘以

n

n

n 的次幂 ; 如 :

n

e

i

−

1

n^{e_i-1}

nei​−1 , 这里有

e

i

e_i

ei​ 个常数 ;

③ 常数 : 常数下标是从

c

i

1

c_{i1}

ci1​ 到

c

i

e

i

c_{ie_i}

ciei​​ , 下标的右侧部分是

1

1

1 到

e

i

e_i

ei​ ;

④

n

n

n 的次幂 : 幂的取值是从

0

0

0 到

e

i

−

1

e_i - 1

ei​−1 ;

⑤ 建议排列方式 : 常数 和 次幂 , 最好都从小到大排列 , 常数下标 与

n

n

n 的幂 相差

1

1

1 ;

( 3 ) 通解第

i

i

i 项 :

H

i

(

n

)

=

(

c

i

1

+

c

i

2

n

+

⋯

+

c

i

e

i

n

e

i

−

1

)

q

i

n

H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n

Hi​(n)=(ci1​+ci2​n+⋯+ciei​​nei​−1)qin​

3 . 写出通解 :

( 1 ) 通解项数 : 特征根数

t

t

t ;

( 2 ) 通解组成 : 每个特征根对应的通解项 , 加到一起 , 就是完整的通解 ;

( 3 ) 最终结果 :

H

(

n

)

=

∑

i

=

1

t

H

i

(

n

)

H(n) = \sum\limits_{i=1}^tH_i(n)

H(n)=i=1∑t​Hi​(n)

三、常系数线性非齐次递推方程 特解形式 ( $n$

---

1 . 特解形式 :

( 1 ) 特解形式 : 特解

H

∗

(

n

)

H^*(n)

H∗(n) 是

n

n

n 的

t

t

t 次多项式 ,

n

n

n 的幂取值从

0

0

0 到

t

t

t , 因此其 项数有

t

+

1

t+1

t+1 项 ;

( 2 ) 特解每项组成 :

① 项数 :

t

+

1

t+1

t+1 项

② 组成 : 特解项由 常数 乘以

n

n

n 的次幂 组成 , 常数是未知的 ;

③ 常数 :

t

+

1

t+1

t+1 个常数 , 使用下标标识好 ;

④

n

n

n 的幂 : 幂取值从

0

0

0 到

t

t

t ;

2 . 举例 : 特解

H

∗

(

n

)

H^*(n)

H∗(n) 是

n

n

n 的

2

2

2 次多项式 ;

特解项数 : 则 特解项数 是

2

+

1

=

3

2 + 1 = 3

2+1=3 项 ;

特解每项组成 : 特解每一项由 常数 乘以

n

n

n 的次幂 组成 ,

• 3

  3

  3 个常数 设为

  P

  1

  ,

  P

  2

  ,

  P

  3

  P_1, P_2, P_3

  P1​,P2​,P3​ ,

• 3

  3

  3 个

  n

  n

  n 的次幂 , 幂取值 从

  0

  0

  0 到

  2

  2

  2 ,

因此特解的形式为

H

∗

(

n

)

=

P

1

n

2

+

P

2

n

1

+

P

3

n

0

H^*(n) = P_1n^2 + P_2n^1 + P_3n^0

H∗(n)=P1​n2+P2​n1+P3​n0 ,

化简后为 :

H

∗

(

n

)

=

P

1

n

2

+

P

2

n

+

P

3

H^*(n) = P_1n^2 + P_2n + P_3

H∗(n)=P1​n2+P2​n+P3​

四、常系数线性非齐次递推方程 特解形式 ( $n$

---

常系数线性非齐次递推方程 :

H

(

n

)

−

a

1

H

(

n

−

1

)

−

⋯

−

a

k

H

(

n

−

k

)

=

f

(

n

)

H(n) - a_1H(n-1) - \cdots - a_kH(n-k) = f(n)

H(n)−a1​H(n−1)−⋯−ak​H(n−k)=f(n) ,

n

≥

k

,

a

k

≠

0

,

f

(

n

)

≠

0

n\geq k , a_k\not= 0, f(n) \not= 0

n≥k,ak​​=0,f(n)​=0

上述方程左侧 与 “常系数线性齐次递推方程” 是一样的 , 但是右侧不是

0

0

0 , 而是一个基于

n

n

n 的 函数

f

(

n

)

f(n)

f(n) , 这种类型的递推方程称为 “常系数线性非齐次递推方程” ;

特解与 “常系数线性非齐次递推方程” 中的右部

f

(

n

)

f(n)

f(n) 有关 ,

f

(

n

)

f(n)

f(n) 为

n

n

n 的

t

t

t 次多项式 ,

如果齐次部分 特征根 不为

1

1

1 , 则特解

H

∗

(

n

)

H^*(n)

H∗(n) 也 是

n

n

n 的

t

t

t 次多项式 ;

如果齐次部分 特征根 为

1

1

1 , 重复度为

e

e

e , 则特解

H

∗

(

n

)

H^*(n)

H∗(n) 也 是

n

n

n 的

t

+

e

t + e

t+e 次多项式 ;

提高的次幂是 特征根

1

1

1 的重复度 , 如果重复度为

2

2

2 , 则需要提高

2

2

2 次幂 ;

为了解决上述问题 , 这里需要将

n

n

n 的次幂提高

1

1

1 , 将特解形式中的一次方项 , 设置成平方项 , 其中常数项不设置 , 即使设置了也会抵消掉 , 无法求出常数项值 ;

五、常系数线性非齐次递推方程 特解形式 ( 非齐次部分是指数 | 底不为特征根 )

---

常系数线性非齐次递推方程 :

H

(

n

)

−

a

1

H

(

n

−

1

)

−

⋯

−

a

k

H

(

n

−

k

)

=

f

(

n

)

H(n) - a_1H(n-1) - \cdots - a_kH(n-k) = f(n)

H(n)−a1​H(n−1)−⋯−ak​H(n−k)=f(n) ,

n

≥

k

,

a

k

≠

0

,

f

(

n

)

≠

0

n\geq k , a_k\not= 0, f(n) \not= 0

n≥k,ak​​=0,f(n)​=0

上述方程左侧 与 “常系数线性齐次递推方程” 是一样的 , 但是右侧不是

0

0

0 , 而是一个基于

n

n

n 的 函数

f

(

n

)

f(n)

f(n) , 这种类型的递推方程称为 “常系数线性非齐次递推方程” ;

非齐次部分是指数的情况 :

如果上述 “常系数线性非齐次递推方程” 的 非齐次部分

f

(

n

)

f(n)

f(n) 是指数函数 ,

β

n

\beta^n

βn ,

如果

β

\beta

β 不是特征根 ,

则非齐次部分的特解形式为 :

H

∗

(

n

)

=

P

β

n

H^*(n) = P\beta^n

H∗(n)=Pβn ,

P

P

P 是常数 ;

将上述特解

H

∗

(

n

)

=

P

β

n

H^*(n) = P\beta^n

H∗(n)=Pβn , 代入递推方程 , 求解出常数

P

P

P 的值 , 进而得到了完整的特解 ;

“常系数线性非齐次递推方程” 的通解是

H

(

n

)

=

H

(

n

)

‾

+

H

∗

(

n

)

H(n) = \overline{H(n)} + H^*(n)

H(n)=H(n)​+H∗(n)

使用上述解出的 特解 , 与递推方程 齐次部分的通解 , 组成递推方程的完整通解 ;

六、常系数线性非齐次递推方程 特解形式 ( 非齐次部分是指数 | 底是特征根 )

---

常系数线性非齐次递推方程 :

H

(

n

)

−

a

1

H

(

n

−

1

)

−

⋯

−

a

k

H

(

n

−

k

)

=

f

(

n

)

H(n) - a_1H(n-1) - \cdots - a_kH(n-k) = f(n)

H(n)−a1​H(n−1)−⋯−ak​H(n−k)=f(n) ,

n

≥

k

,

a

k

≠

0

,

f

(

n

)

≠

0

n\geq k , a_k\not= 0, f(n) \not= 0

n≥k,ak​​=0,f(n)​=0

上述方程左侧 与 “常系数线性齐次递推方程” 是一样的 , 但是右侧不是

0

0

0 , 而是一个基于

n

n

n 的 函数

f

(

n

)

f(n)

f(n) , 这种类型的递推方程称为 “常系数线性非齐次递推方程” ;

非齐次部分是 指数函数 且 底是特征根的情况 :

如果上述 “常系数线性非齐次递推方程” 的 非齐次部分

f

(

n

)

f(n)

f(n) 是指数函数 ,

β

n

\beta^n

βn ,

如果

β

\beta

β 是

e

e

e 重特征根 ,

非齐次部分的特解形式为 :

H

∗

(

n

)

=

P

n

e

β

n

H^*(n) = P n^e \beta^n

H∗(n)=Pneβn ,

P

P

P 是常数 ;

将上述特解

H

∗

(

n

)

=

P

n

e

β

n

H^*(n) = P n^e \beta^n

H∗(n)=Pneβn , 代入递推方程 , 求解出常数

P

P

P 的值 , 进而得到了完整的特解 ;

“常系数线性非齐次递推方程” 的通解是

H

(

n

)

=

H

(

n

)

‾

+

H

∗

(

n

)

H(n) = \overline{H(n)} + H^*(n)

H(n)=H(n)​+H∗(n)

使用上述解出的 特解 , 与递推方程 齐次部分的通解 , 组成递推方程的完整通解 ;