文章目录
- 一、非降路径问题 概要说明
- 二、非降路径问题 基本模型
- 二、非降路径问题 拓展模型 1
- 三、非降路径问题 拓展模型 2
组合恒等式参考博客 :
- 【组合数学】二项式定理与组合恒等式 ( 二项式定理 | 三个组合恒等式 递推式 | 递推式 1 | 递推式 2 | 递推式 3 帕斯卡/杨辉三角公式 | 组合分析方法 | 递推式组合恒等式特点 )
- 【组合数学】组合恒等式 ( 递推 组合恒等式 | 变下项求和 组合恒等式 简单和 | 变下项求和 组合恒等式 交错和 )
- 【组合数学】组合恒等式 ( 变下项求和 3 组合恒等式 | 变下项求和 4 组合恒等式 | 二项式定理 + 求导 证明组合恒等式 | 使用已知组合恒等式证明组合恒等式 )
- 【组合数学】组合恒等式 ( 八个组合恒等式回顾 | 组合恒等式 积 1 | 证明 | 使用场景 )
- 【组合数学】组合恒等式 ( 组合恒等式 积之和 1 | 积之和 1 证明 | 组合恒等式 积之和 2 | 积之和 2 证明 )
一、非降路径问题 概要说明
非降路径问题 是组合计数模型 , 利用该组合计数模型 , 可以处理一些常见的组合计数问题 ;
非降路径问题 :
( 1 ) 基本模型
( 2 ) 在限制条件下的非降路径个数
( 3 ) 非降路径模型应用
- ① 证明恒等式
- ② 单调函数计数
- ③ 栈输出
二、非降路径问题 基本模型
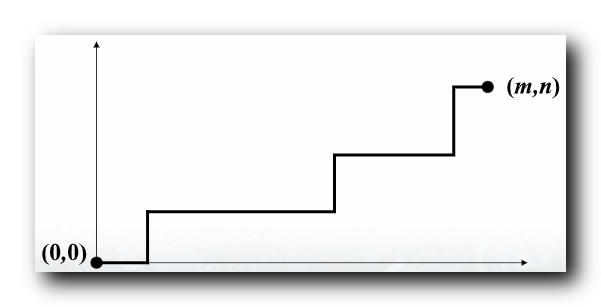
计算 从
(
0
,
0
)
(0,0)
(0,0) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数 ?
1 . 非降路径要求 :
出发点 : 从
(
0
,
0
)
(0,0)
(0,0) 出发 ;
移动坐标要求 : 向右走 整数坐标 , 水平和垂直坐标都走 整数长度 ;
移动方向要求 : 每次只能向右 , 或者向上移动 ; 不能向左 , 向下走 ;
2 . 转为选取问题 : 将其变成一个选取问题 ,
步数分析 : 从
(
0
,
0
)
(0,0)
(0,0) 到
(
m
,
n
)
(m, n)
(m,n) , 向右要走
m
m
m 步 , 向上要走
n
n
n 步 ;
选取问题说明 : 总共走
m
+
n
m+n
m+n 步 , 需要选择那些步向上 , 哪些步向右 , 只要在之和
m
+
n
m + n
m+n 步中 , 将向右的
m
m
m 步都标定后 , 剩下的就是向上的步了 ;
选取问题组合数计算 : 因此这里只要 从
m
+
n
m+n
m+n 步中选取
m
m
m 步即可 , 结果是
C
(
m
+
n
,
m
)
C(m+n, m)
C(m+n,m) , 又可以写成
(
m
+
n
m
)
\dbinom{m + n}{m}
(mm+n)
二、非降路径问题 拓展模型 1
计算 从
(
a
,
b
)
(a,b)
(a,b) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数 ?
上述 从
(
a
,
b
)
(a,b)
(a,b) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径数 ,
等于
从
(
0
,
0
)
(0,0)
(0,0) 到
(
m
−
a
,
n
−
b
)
(m-a, n-b)
(m−a,n−b) 的非降路径数 ;
坐标平移 : 上述的原理是 坐标平移 , 将整体坐标 向左平移
a
a
a , 向下平移
b
b
b , 即可得到 从
(
0
,
0
)
(0,0)
(0,0) 到
(
m
−
a
,
n
−
b
)
(m-a, n-b)
(m−a,n−b) 的 非降路径问题基本模型 ;
因此 从
(
a
,
b
)
(a,b)
(a,b) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数为
C
(
m
−
a
+
n
−
b
,
m
−
a
)
C(m-a + n-b , m-a)
C(m−a+n−b,m−a) 条 ;
三、非降路径问题 拓展模型 2
计算 从
(
a
,
b
)
(a,b)
(a,b) 经过
(
c
,
d
)
(c, d)
(c,d) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数 ?
1 . 计算过程说明 :
( 1 ) 分步处理 : 使用 分步计数原理 , 对应乘法法则 ;
( 2 ) 第一步 : 先计算从
(
a
,
b
)
(a,b)
(a,b) 到
(
c
,
d
)
(c, d)
(c,d) 的非降路径条数 ;
( 3 ) 第二步 : 然后计算从
(
c
,
d
)
(c, d)
(c,d) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数 ;
( 4 ) 乘法法则 : 根据乘法法则 , 将上述两个结果相乘 , 最终就是结果要求的非降路径条数 ;
2 . 计算第一步
计算从
(
a
,
b
)
(a,b)
(a,b) 到
(
c
,
d
)
(c, d)
(c,d) 的非降路径条数 , 代入之前的 公式
从
(
a
,
b
)
(a,b)
(a,b) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数为
C
(
m
−
a
+
n
−
b
,
m
−
a
)
C(m-a + n-b , m-a)
C(m−a+n−b,m−a) 条
结果为 :
C
(
c
−
a
+
c
−
b
,
c
−
a
)
C(c-a + c-b , c-a)
C(c−a+c−b,c−a)
3 . 计算第二步
计算从
(
c
,
d
)
(c,d)
(c,d) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数 , 代入之前的 公式
从
(
a
,
b
)
(a,b)
(a,b) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数为
C
(
m
−
a
+
n
−
b
,
m
−
a
)
C(m-a + n-b , m-a)
C(m−a+n−b,m−a) 条
结果为 :
C
(
m
−
c
+
n
−
d
,
m
−
c
)
C(m-c + n-d , m-c)
C(m−c+n−d,m−c)
4 . 乘法法则
将上述两个非降路径数相乘 , 就是最终结果 ;
从
(
a
,
b
)
(a,b)
(a,b) 经过
(
c
,
d
)
(c, d)
(c,d) 到
(
m
,
n
)
(m, n)
(m,n) 的非降路径条数是 :
C
(
c
−
a
+
c
−
b
,
c
−
a
)
C
(
m
−
c
+
n
−
d
,
m
−
c
)
C(c-a + c-b , c-a) C(m-c + n-d , m-c)
C(c−a+c−b,c−a)C(m−c+n−d,m−c)
 IDEA激活码
IDEA激活码


