容斥原理 示例
24
24
24 个人
说英语 , 日语 , 德语 , 法语 的人数
13
,
5
,
10
,
9
13, 5, 10, 9
13,5,10,9
同时说 英语 日语 人数
2
2
2
同时说 英语 德语 人数
4
4
4
同时说 英语 法语 人数
4
4
4
同时说 法语 德语 人数
4
4
4
说日语的人 不会 法语 德语 ;
求 只会说一种语言的人 ? 同时会说 英语 德语 法语 的人 ?
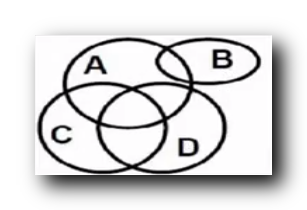
单个语言集合 :
A
A
A 集合表示会说英语的人的集合 ,
∣
A
∣
=
13
|A| = 13
∣A∣=13 ;
B
B
B 集合表示会说日语的人的集合 ,
∣
B
∣
=
5
|B| = 5
∣B∣=5 ;
C
C
C 集合表示会说德语的人的集合 ,
∣
C
∣
=
10
|C| = 10
∣C∣=10 ;
D
D
D 集合表示会说法语的人的集合 ,
∣
D
∣
=
9
|D| = 9
∣D∣=9 ;
两两相交集合 :
A
∩
B
A \cap B
A∩B 集合表示会说 英语 日语 的人的集合 ,
∣
A
∩
B
∣
=
2
|A \cap B| = 2
∣A∩B∣=2 ;
A
∩
C
A \cap C
A∩C 集合表示会说 英语 德语 的人的集合 ,
∣
A
∩
C
∣
=
4
|A \cap C| = 4
∣A∩C∣=4 ;
A
∩
D
A \cap D
A∩D 集合表示会说 英语 法语 的人的集合 ,
∣
A
∩
D
∣
=
4
|A \cap D| = 4
∣A∩D∣=4 ;
C
∩
D
C \cap D
C∩D 集合表示会说 德语 法语 的人的集合 ,
∣
C
∩
D
∣
=
4
|C \cap D| = 4
∣C∩D∣=4 ;
会说日语的人 , 既不不会说法语 , 也不会说德语 , 说明集合
B
B
B 与集合
C
,
D
C, D
C,D 都不相交 ;
∣
B
∩
C
∣
=
∣
B
∩
D
∣
=
∣
A
∩
B
∩
C
∣
=
∣
A
∩
B
∩
D
∣
=
∣
B
∩
C
∩
D
∣
=
∣
A
∩
B
∩
C
∩
D
∣
=
0
|B \cap C| = |B \cap D| = |A \cap B \cap C| = |A \cap B \cap D| = |B \cap C \cap D| = |A \cap B \cap C \cap D| = 0
∣B∩C∣=∣B∩D∣=∣A∩B∩C∣=∣A∩B∩D∣=∣B∩C∩D∣=∣A∩B∩C∩D∣=0
总的人数是
24
24
24 人 :
∣
A
∪
B
∪
C
∪
D
∣
=
24
|A \cup B \cup C \cup D| = 24
∣A∪B∪C∪D∣=24
根据容斥原理 :
∣
A
∪
B
∪
C
∪
D
∣
=
|A \cup B \cup C \cup D| =
∣A∪B∪C∪D∣=
∣
A
∣
+
∣
B
∣
+
∣
C
∣
+
∣
D
∣
| A | + | B | + | C | + | D |
∣A∣+∣B∣+∣C∣+∣D∣ 先将单个集合的个数相加
−
(
∣
A
∩
B
∣
+
∣
A
∩
C
∣
+
∣
A
∩
D
∣
+
∣
B
∩
C
∣
+
∣
B
∩
D
∣
+
∣
C
∩
D
∣
)
- ( | A \cap B | + | A \cap C | + | A \cap D | + | B \cap C | + | B \cap D | + | C \cap D |)
−(∣A∩B∣+∣A∩C∣+∣A∩D∣+∣B∩C∣+∣B∩D∣+∣C∩D∣) 减去两两相交的元素个数
+
(
∣
A
∩
B
∩
C
∣
+
∣
A
∩
B
∩
D
∣
+
∣
A
∩
C
∩
D
∣
+
∣
B
∩
C
∩
D
∣
)
+ ( | A \cap B \cap C | + | A \cap B \cap D | + | A \cap C \cap D | + | B \cap C \cap D |)
+(∣A∩B∩C∣+∣A∩B∩D∣+∣A∩C∩D∣+∣B∩C∩D∣) 加上三三相交的元素个数
−
∣
A
∩
B
∩
C
∩
D
∣
- |A \cap B \cap C \cap D|
−∣A∩B∩C∩D∣ 减去 四个集合相交的元素个数
=
24
= 24
=24
将上面的集合元素个数全部代入 :
∣
A
∪
B
∪
C
∪
D
∣
=
|A \cup B \cup C \cup D| =
∣A∪B∪C∪D∣=
13
+
5
+
10
+
9
13 + 5 + 10 + 9
13+5+10+9 先将单个集合的个数相加
−
(
2
+
4
+
4
+
0
+
0
+
4
)
- ( 2 + 4 + 4 + 0 + 0 + 4 )
−(2+4+4+0+0+4) 减去两两相交的元素个数
+
(
0
+
0
+
∣
A
∩
C
∩
D
∣
+
0
)
+ ( 0 + 0 + | A \cap C \cap D | + 0 )
+(0+0+∣A∩C∩D∣+0) 加上三三相交的元素个数
−
0
- 0
−0 减去 四个集合相交的元素个数
=
24
= 24
=24
计算后得到 :
37
−
14
+
∣
A
∩
C
∩
D
∣
=
24
37 - 14 + | A \cap C \cap D | = 24
37−14+∣A∩C∩D∣=24
∣
A
∩
C
∩
D
∣
=
1
| A \cap C \cap D | = 1
∣A∩C∩D∣=1
同时会说英法德语的人
∣
A
∩
C
∩
D
∣
=
1
| A \cap C \cap D | = 1
∣A∩C∩D∣=1 只有
1
1
1 个 ;
计算只会说英语的人 :
∣
A
∣
−
∣
(
B
∪
C
∪
D
)
∩
A
∣
| A | - | ( B \cup C \cup D ) \cap A |
∣A∣−∣(B∪C∪D)∩A∣
=
∣
A
∣
−
∣
(
B
∩
A
)
∪
(
C
∩
A
)
∪
(
D
∩
A
)
∣
= |A| - | (B \cap A) \cup ( C \cap A ) \cup ( D \cap A ) |
=∣A∣−∣(B∩A)∪(C∩A)∪(D∩A)∣
使用容斥原理 , 计算
∣
(
B
∩
A
)
∪
(
C
∩
A
)
∪
(
D
∩
A
)
∣
| (B \cap A) \cup ( C \cap A ) \cup ( D \cap A ) |
∣(B∩A)∪(C∩A)∪(D∩A)∣
∣
(
B
∩
A
)
∪
(
C
∩
A
)
∪
(
D
∩
A
)
∣
| (B \cap A) \cup ( C \cap A ) \cup ( D \cap A ) |
∣(B∩A)∪(C∩A)∪(D∩A)∣
=
(
∣
B
∩
A
∣
+
∣
C
∩
A
∣
+
∣
D
∩
A
∣
)
= ( |B \cap A| + |C \cap A| + |D \cap A| )
=(∣B∩A∣+∣C∩A∣+∣D∩A∣)
−
(
∣
A
∩
B
∩
C
∣
+
∣
A
∩
B
∩
D
∣
+
∣
A
∩
C
∩
D
∣
)
- ( | A \cap B \cap C | + | A \cap B \cap D | + | A \cap C \cap D |)
−(∣A∩B∩C∣+∣A∩B∩D∣+∣A∩C∩D∣)
+
(
∣
A
∩
B
∩
C
∩
D
∣
)
+ ( |A \cap B \cap C \cap D| )
+(∣A∩B∩C∩D∣)
=
(
2
+
4
+
4
)
−
(
0
+
0
+
1
)
+
(
0
)
=
9
= ( 2 + 4 + 4) - ( 0 + 0 + 1 ) + ( 0 ) = 9
=(2+4+4)−(0+0+1)+(0)=9
∣
A
∣
−
∣
(
B
∪
C
∪
D
)
∩
A
∣
=
∣
A
∣
−
∣
(
B
∩
A
)
∪
(
C
∩
A
)
∪
(
D
∩
A
)
∣
=
13
−
9
=
4
| A | - | ( B \cup C \cup D ) \cap A |= |A| - | (B \cap A) \cup ( C \cap A ) \cup ( D \cap A ) | = 13 - 9 = 4
∣A∣−∣(B∪C∪D)∩A∣=∣A∣−∣(B∩A)∪(C∩A)∪(D∩A)∣=13−9=4
只会说英语的人有
4
4
4 个 ;
按照上述步骤 , 计算出 其它 只说日语的人
3
3
3 个 , 只说 德语 的人 3 个 , 只说法语的人
2
2
2 个 ;
 IDEA激活码
IDEA激活码


