文章目录
- 一、鸽巢原理简单形式示例 4
- 二、鸽巢原理简单形式示例 5
一、鸽巢原理简单形式示例 4
假设有
3
3
3 个
7
7
7 位二进制数 ,
A
:
a
1
a
2
a
3
a
4
a
5
a
6
a
7
A : a_1a_2a_3a_4a_5a_6a_7
A:a1a2a3a4a5a6a7
B
:
b
1
b
2
b
3
b
4
b
5
b
6
b
7
B : b_1b_2b_3b_4b_5b_6b_7
B:b1b2b3b4b5b6b7
C
:
c
1
c
2
c
3
c
4
c
5
c
6
c
7
C : c_1c_2c_3c_4c_5c_6c_7
C:c1c2c3c4c5c6c7
证明存在整数
i
i
i 和
j
j
j ,
1
≤
i
≤
j
≤
7
1\leq i \leq j \leq 7
1≤i≤j≤7 , 使得下列之一一定成立 :
a
i
=
a
j
=
b
i
=
b
j
a_i = a_j = b_i = b_j
ai=aj=bi=bj
a
i
=
a
j
=
c
i
=
c
j
a_i = a_j = c_i = c_j
ai=aj=ci=cj
b
i
=
b
j
=
c
i
=
c
j
b_i = b_j = c_i = c_j
bi=bj=ci=cj
证明 :
二进制数 , 取值只能是
0
0
0 或
1
1
1 ;
使用表格图形表示
A
B
C
ABC
ABC 三个二进制数的
7
7
7 位 : 使用二进制数
0
,
1
0,1
0,1 填写这些位 ;
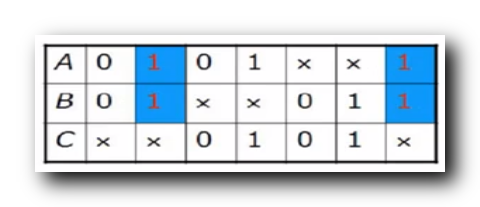
上图中 :
- 第
1
1
1 行是 二进制数字A
A
A 的7
7
7 位 ; - 第
2
2
2 行是 二进制数字B
B
B 的7
7
7 位 ; - 第
3
3
3 行是 二进制数字C
C
C 的7
7
7 位 ;
使用二进制数
0
,
1
0,1
0,1 填写表格中的这些位 ;
总结出以下模式 : 以列为单位 , 总结出一定的模式 , 下面的模式中每一列的第
1
∼
3
1 \sim 3
1∼3 行取值为某数 ;
-
①
1
−
2
−
0
1-2-0
1−2−0 : 某列 第
1
1
1 行 , 第
2
2
2 行 , 取值为
0
0
0 , 第
3
3
3 行取值随意 ;

-
②
1
−
2
−
1
1-2-1
1−2−1 : 某列 第
1
1
1 行 , 第
2
2
2 行 , 取值为
1
1
1 , 第
3
3
3 行取值随意 ;

-
③
1
−
3
−
0
1-3-0
1−3−0 : 某列 第
1
1
1 行 , 第
3
3
3 行 , 取值为
0
0
0 , 第
2
2
2 行取值随意 ;

-
④
1
−
3
−
1
1-3-1
1−3−1 : 某列 第
1
1
1 行 , 第
3
3
3 行 , 取值为
1
1
1 , 第
2
2
2 行取值随意 ;

-
⑤
2
−
3
−
0
2-3-0
2−3−0 : 某列 第
2
2
2 行 , 第
3
3
3 行 , 取值为
0
0
0 , 第
1
1
1 行取值随意 ;

-
⑥
2
−
3
−
1
2-3-1
2−3−1 : 某列 第
2
2
2 行 , 第
3
3
3 行 , 取值为
1
1
1 , 第
1
1
1 行取值随意 ;

有以上
6
6
6 种可能的模式 , 但是二进制数有
7
7
7 位 ;
可以等价理解为鸽巢原理的 : 将
7
7
7 个物体放到
6
6
6 个盒子中 , 则 至少有一个盒子中有
2
2
2 个 或
2
2
2 个以上的物体 ;
因此至少有
2
2
2 列或
2
2
2 列以上的模式相同 ;
模式相同的两列中 , 还有四角数字相同的矩形 , 四角方格数字满足相同的要求 ;
因此 , 必定存在整数
i
i
i 和
j
j
j ,
1
≤
i
≤
j
≤
7
1\leq i \leq j \leq 7
1≤i≤j≤7 , 使得下列之一一定成立 :
a
i
=
a
j
=
b
i
=
b
j
a_i = a_j = b_i = b_j
ai=aj=bi=bj
a
i
=
a
j
=
c
i
=
c
j
a_i = a_j = c_i = c_j
ai=aj=ci=cj
b
i
=
b
j
=
c
i
=
c
j
b_i = b_j = c_i = c_j
bi=bj=ci=cj
二、鸽巢原理简单形式示例 5
证明 :
1
1
1 到
2
n
2n
2n 的正整数中 , 任取
n
+
1
n + 1
n+1 个数 , 至少有一对数 , 其中一个数是另外一个数的倍数 ;
使用如下形式表示
1
1
1 到
2
n
2n
2n 的正整数 ;
上述数字每个数字 , 除以
2
α
i
2^{\alpha_i}
2αi , 会得到一个奇数
r
i
r_i
ri ;
使用
a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri ,
i
=
1
,
2
,
⋯
,
n
+
1
i = 1, 2, \cdots , n+1
i=1,2,⋯,n+1 形式表示上述
1
1
1 到
2
n
2n
2n 的正整数 ;
1
1
1 到
2
n
2n
2n 的正整数表示说明 : ( 仅做参考 )
- 表示奇数 : 奇数
r
i
r_i
ri 就等于表示的正整数值 ,2
α
i
=
1
2^{\alpha_i} = 1
2αi=1 , 即α
i
=
0
\alpha_i = 0
αi=0 ; - 表示偶数 : 如果是偶数 , 至少能除以一个
2
2
2 ,2
α
i
≥
2
2^{\alpha_i} \geq 2
2αi≥2 , 即α
i
≥
1
\alpha_i \geq 1
αi≥1 ;
1
1
1 到
2
n
2n
2n 的正整数 中 , 有
n
n
n 个奇数 , 是
1
,
3
,
5
,
7
,
9
,
⋯
,
2
n
−
1
1, 3, 5, 7, 9, \cdots , 2n - 1
1,3,5,7,9,⋯,2n−1 ;
每个数
a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri 右侧的
r
i
r_i
ri 奇数 取值只有
n
n
n 种 , 偶数部分的右侧的
r
i
r_i
ri 奇数也包含在其中 ;
现在要从
1
1
1 到
2
n
2n
2n 的正整数 中 取
n
+
1
n+1
n+1 个数 , 如果其中有奇数 , 肯定只有
n
n
n 种取值 ;
将取值看做盒子 , 每个数的右边的
r
i
r_i
ri 看做物体 , 奇数的个数是
n
+
1
n + 1
n+1 个 , 但是奇数的个数只有
n
n
n 种取值 , 因此有两个数字的 奇数部分
r
i
r_i
ri 是相等 ;
假设这两个数分别是第
i
i
i 个数 , 和第
j
j
j 个数 :
r
i
=
r
j
r_i = r_j
ri=rj , 并且
i
<
j
i < j
i<j ;
- 第
i
i
i 个数 :a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri ,i
=
1
,
2
,
⋯
,
n
+
1
i = 1, 2, \cdots , n+1
i=1,2,⋯,n+1 - 第
j
j
j 个数 :a
j
=
2
α
j
r
j
a_j = 2^{\alpha_j}r_j
aj=2αjrj ,j
=
1
,
2
,
⋯
,
n
+
1
j = 1, 2, \cdots , n+1
j=1,2,⋯,n+1
如果
r
i
=
r
j
r_i = r_j
ri=rj , 那么
2
α
j
2^{\alpha_j}
2αj 肯定是
2
α
i
2^{\alpha_i}
2αi 的倍数 ;
 IDEA激活码
IDEA激活码


