文章目录
- 一、鸽巢原理简单形式
- 二、鸽巢原理简单形式示例 1
- 三、鸽巢原理简单形式示例 2
- 四、鸽巢原理简单形式示例 3
一、鸽巢原理简单形式
鸽巢原理 :
将
n
+
1
n + 1
n+1 个物体 放到
n
n
n 个盒子 中 , 则
一定存在一个盒子 中 至少 含有
2
2
2 个 或
2
2
2 个以上的物体 ;
鸽巢原理 实际上是 多对少的配置 ; 至少存在一个多对一的情况 ;
二、鸽巢原理简单形式示例 1
证明 : 在边长为
2
2
2 的正三角形中 , 有
5
5
5 个点 , 一定存在两个点的距离小于
1
1
1 ;
将变成为
2
2
2 的正三角形 , 分为
4
4
4 个小的正三角形 , 每个边长为
1
1
1 ; 如下图 :
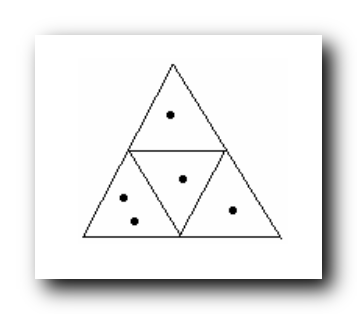
在
4
4
4 个小正方形中 , 绘制
5
5
5 个点 ;
根据鸽巢原理 , 上述问题可以转为 将
5
5
5 个物体放入
4
4
4 个盒子中 , 至少有一个盒子中有
2
2
2 个 或
2
2
2 个以上的物体 ;
在一个正三角形格子中 , 如果绘制了两个点 , 其距离肯定小于
1
1
1 ;
三、鸽巢原理简单形式示例 2
证明 :
9
×
3
9\times3
9×3 的方格 , 使用黑色 , 白色 两种颜色进行涂色 , 必定存在两列相同的涂色方案 ;
先将可能的涂色方案枚举出来 : 一共只可能存在
2
3
=
8
2^3 = 8
23=8 种可能的涂色方案 ;
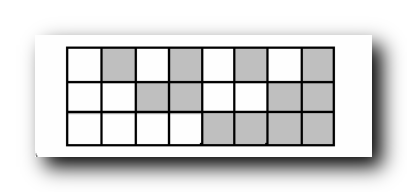
在
9
9
9 列方格中 , 使用
8
8
8 种模式进行涂色 ;
可以等价理解为鸽巢原理的 : 将
9
9
9 个物体放到
8
8
8 个盒子中 , 则 至少有一个盒子中有
2
2
2 个 或
2
2
2 个以上的物体 ;
因此至少有
2
2
2 列或
2
2
2 列以上的格子会被涂成一种颜色 ;
四、鸽巢原理简单形式示例 3
证明 : 空间中有
9
9
9 个格点 , 所有的两点连线的中点 , 有一个格点 ;
格点指的是整数点 ;
连线中点是格点的要求 : 空间坐标
(
x
,
y
,
z
)
(x,y,z)
(x,y,z) 与
(
x
′
,
y
′
,
z
′
)
(x' , y' , z')
(x′,y′,z′) 有相同的奇偶性 , 即
-
x
,
x
′
x , x'
x,x′ 同为奇数或偶数 , -
y
,
y
′
y , y'
y,y′ 同为奇数或偶数 , -
z
,
z
′
z , z'
z,z′ 同为奇数或偶数 ,
此时这两个空间坐标的连线中点就是 格点 , 即整数点 ;
下面分析三个坐标分别奇偶性相同时 , 中点是格点的原因 :
连线中点坐标公式为 :
(
x
+
x
′
2
,
y
+
y
′
2
,
z
+
z
′
2
)
( \dfrac{x + x'}{2} , \dfrac{y + y'}{2} , \dfrac{z + z'}{2} )
(2x+x′,2y+y′,2z+z′)
当奇偶性相同的时候 , 连线中点的空间坐标的三个数都是整数 ;
空间坐标
(
x
,
y
,
z
)
(x,y,z)
(x,y,z) 与
(
x
′
,
y
′
,
z
′
)
(x' , y' , z')
(x′,y′,z′) 的奇偶模式有
2
3
=
8
2^3 = 8
23=8 种 ; 分别是
- 第
1
1
1 个坐标x
,
x
′
x , x'
x,x′ 奇偶相同 / 不同 , 两种情况 ; - 第
2
2
2 个坐标y
,
y
′
y , y'
y,y′ 奇偶相同 / 不同 , 两种情况 ; - 第
3
3
3 个坐标z
,
z
′
z , z'
z,z′ 奇偶相同 / 不同 , 两种情况 ;
上述每个坐标有两种情况 , 三个坐标下来就是
2
×
2
×
2
=
8
2 \times 2 \times 2 = 8
2×2×2=8 种情况 , 这是乘法原则 ;
空间中
9
9
9 个格点 , 每个格点的奇偶模式有
8
8
8 种 ;
可以等价理解为鸽巢原理的 : 将
9
9
9 个物体放到
8
8
8 个盒子中 , 则 至少有一个盒子中有
2
2
2 个 或
2
2
2 个以上的物体 ;
因此至少有
2
2
2 个或
2
2
2 个以上的格点的奇偶模式是相同的 ;
因此 :
2
2
2 个奇偶模式相同的格点连接的中点 , 肯定是格点 ;
 IDEA激活码
IDEA激活码


