一、组合思想 3 : 上下界逼近

---

上下界逼近 的思想 , 通常用于 确定某个值 , 或 确定某个函数的阶 ( 函数的量级 ) ;

上下界逼近 步骤 :

( 1 ) 证明值的上界

( 2 ) 证明值的下界

( 3 ) 如果 上界与下界值相等 , 则 证明结束

( 4 ) 如果 上界与下界值不相等 , 则 改进上界 或 下界 , 使这两个值逐渐逼近 ;

组合数学中很多组合数的值 , 有些上下界相等 , 得到了精确的值 , 有些只得到了组合数的上界和下界 , 并且 上界下界不相等 , 具体值未知 ;

二、上下界逼近示例 ( Remsey 数 )

---

Remsey ( 莱姆希 ) 数

K

n

K_n

Kn​ 是完全

n

n

n 阶图 , 完全图就是 每对不同的顶点之间都有一条边 , 即每个顶点都有连接到其它所有顶点的边 ;

使用红蓝两种颜色 , 对

K

n

K_n

Kn​ 的边进行涂色 , 求 在涂色中 , 出现 一个红色三角形 或 一个蓝色三角形 的

n

n

n 的最小值 ;

结果是

6

6

6 ;

这个

6

6

6 就是上界 ;

对

K

6

K_6

K6​ 完全图进行涂色 , 不管怎么涂色 , 都会出现 一个红色三角形 或 一个蓝色三角形 ;

K

6

K_6

K6​ 完全图中 , 根据完全图定义 , 每对不同的顶点之间都有一条边 ,

每个顶点都关联着五条边 , 这

5

5

5 条边 , 必须使用两种颜色对这

5

5

5 条边 进行涂色 , 红色 或 蓝色 , 同种颜色的边至少有

3

3

3 条 ( 或者

3

3

3 条红色 , 或者

3

3

3 条蓝色 ) ,

1. 假定该顶点关联的边有

3

3

3 条是红色的 , 下图是一个顶点引出

3

3

3 条红色的边 , 这三条红边的另外一端的三个顶点 , 有三条边 , 下面讨论这三条边的情况 :

假如三条边都是蓝边 , 如下图 , 那么构成一个蓝色三角形 ;

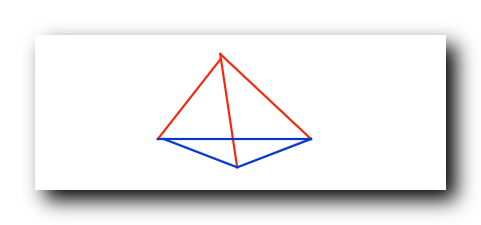
假如三条边有一条红边 , 如下图 , 那么构成一个红色三角形 ;

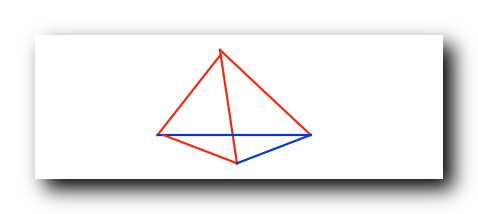
2. 假定该顶点关联的边有

3

3

3 条是蓝色的 , 下图是一个顶点引出

3

3

3 条蓝色的边 , 这三条蓝边的另外一端的三个顶点 , 有三条边 , 下面讨论这三条边的情况 :

假如三条边都是红边 , 如下图 , 那么构成一个红色三角形 ;

假如三条边有一条蓝边 , 如下图 , 那么构成一个来蓝色三角形 ;

K

n

K_n

Kn​ 完全图总的

n

=

6

n = 6

n=6 数值就是上界 ,

n

=

7

n = 7

n=7 更没有问题 ;

上界问题确定了 , 现在讨论下界 ;

讨论

n

=

5

n = 5

n=5 的情况 :

举出一个反例 , 下图中的涂色方案中 , 既没有蓝色三角形 , 也没有红色三角形 , 因此

n

=

5

n=5

n=5 时 , “出现 一个红色三角形 或 一个蓝色三角形” 不成立 ;

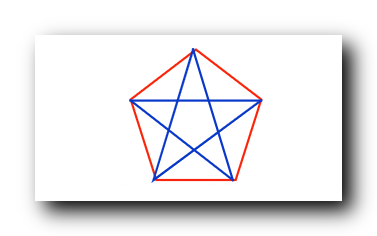
因此

n

=

6

n=6

n=6 是下界 , 不能存在比

6

6

6 小的值 ;