文章目录
- 一、组合思想 2 : 数学归纳法
- 二、数学归纳法推广
- 三、多重归纳思想
一、组合思想 2 : 数学归纳法
数学归纳法 描述 一个与自然数相关的命题
P
(
n
)
P(n)
P(n) ,
根据不同的问题 , 设定
n
n
n 最小的值 , 一般情况下从
0
0
0 开始 ,
1. 证明时分为以下两个步骤 :
( 1 ) 归纳基础 : 先证明 归纳基础 , 如证明
P
(
0
)
P(0)
P(0) 为真 ;
( 2 ) 归纳步骤 : 根据 数学归纳法的种类 , 进行不同方式的证明 , 这里有 第一数学归纳法 和 第二数学归纳法 两种归纳法 ;
2. 数学归纳法 :
( 1 ) 第一数学归纳法 : 从
P
(
n
)
P(n)
P(n) 推导
P
(
n
+
1
)
P(n + 1)
P(n+1)
P
(
0
)
P(0)
P(0) 为真
假设
P
(
n
)
P(n)
P(n) 为真 , 证明
P
(
n
+
1
)
P(n + 1)
P(n+1) 也为真
( 2 ) 第二数学归纳法 : 所有小于
n
n
n 的
P
(
0
)
,
P
(
1
)
,
⋯
,
P
(
n
−
1
)
P(0) , P(1), \cdots , P(n-1)
P(0),P(1),⋯,P(n−1) 都为真 , 推导
P
(
n
)
P(n)
P(n) 为真 ;
P
(
0
)
P(0)
P(0) 为真
假设所有小于
n
n
n 的自然数
k
k
k , 命题
P
(
k
)
P(k)
P(k) 都为真 , 即
P
(
0
)
,
P
(
1
)
,
⋯
,
P
(
n
−
1
)
P(0) , P(1), \cdots , P(n-1)
P(0),P(1),⋯,P(n−1) 都为真 , 推导
P
(
n
)
P(n)
P(n) 为真 ;
符号化表示为 :
P
(
0
)
∧
P
(
1
)
∧
⋯
∧
P
(
n
−
1
)
→
P
(
n
)
P(0) \land P(1) \land \cdots \land P(n-1) \to P(n)
P(0)∧P(1)∧⋯∧P(n−1)→P(n)
二、数学归纳法推广
数学归纳法可以推广 , 组合中可能遇到出现 两个自然数的问题 , 因此 对应的命题是两个自然数
P
(
m
,
n
)
P(m,n)
P(m,n) , 之前的命题都是一个自然数
P
(
n
)
P(n)
P(n) ;
1. 证明两个自然数的命题
P
(
m
,
n
)
P(m,n)
P(m,n)
针对该
m
,
n
m,n
m,n 两个自然数 ,
任意给定其中一个自然数
m
m
m , 即
m
m
m 可以是任意大小的自然数 , 对
n
n
n 归纳 ;
或
任意给定其中一个自然数
n
n
n , 即
n
n
n 可以是任意大小的自然数 , 对
m
m
m 归纳 ;
任意先指定一个自然数的值 , 对另一个自然数进行归纳 ;
一个自然数的归纳 , 就采用传统的数学归纳法进行归纳证明 ;
2. 多重归纳 :
( 1 ) 归纳基础 : 设置
P
(
m
,
n
)
P(m,n)
P(m,n) 其中某个自然数为
0
0
0 , 另一个自然数是任意大小 ;
P
(
0
,
n
′
)
P(0, n')
P(0,n′) 是归纳基础 ,
m
=
0
m= 0
m=0 ,
n
′
n'
n′ 是任意大小 ;
P
(
m
′
,
0
)
P(m', 0)
P(m′,0) 是归纳基础 ,
n
=
0
n= 0
n=0 ,
m
′
m'
m′ 是任意大小 ;
先证明上述归纳基础为真 ;
( 2 ) 归纳步骤 :
假设
P
(
m
−
1
,
n
)
P(m-1, n)
P(m−1,n) ,
P
(
m
,
n
−
1
)
P(m , n-1)
P(m,n−1) 为真 , 证明
P
(
m
,
n
)
P(m, n)
P(m,n) 为真 ;
三、多重归纳思想
平面坐标系 :
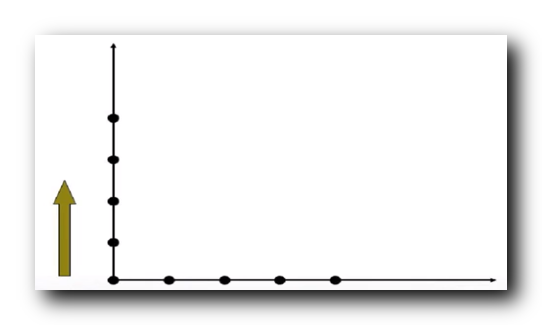
如果
x
=
0
x = 0
x=0 时参数为真 , 即
y
y
y 轴上的 点代表的 参数都为真 ;
如果
y
=
0
y = 0
y=0 时参数为真 , 即
x
x
x 轴上的 点代表的 参数都为真 ;
上述两个坐标轴上的点相当于归纳基础 ;
有了归纳基础后 , 利用坐标轴上的点 , 推导坐标系中间部分的点代表的参数为真 ;
有两个点为真 , 证明比这两个点多
1
1
1 的点为真 , 证明出来 ,
假设
P
(
m
−
1
,
n
)
P(m-1, n)
P(m−1,n) ,
P
(
m
,
n
−
1
)
P(m , n-1)
P(m,n−1) 证明
P
(
m
,
n
)
P(m, n)
P(m,n) 为真
证明
P
(
1
,
1
)
P(1, 1)
P(1,1) 为真 :
P
(
1
−
1
,
1
)
,
P
(
1
,
1
−
1
)
P(1 - 1 , 1) , P(1 , 1 - 1)
P(1−1,1),P(1,1−1) 为真 , 即
P
(
0
,
1
)
,
P
(
1
,
0
)
P(0,1) , P(1, 0)
P(0,1),P(1,0) 为真 ,
可以推导出
P
(
1
,
1
)
P(1,1)
P(1,1) 为真 ;
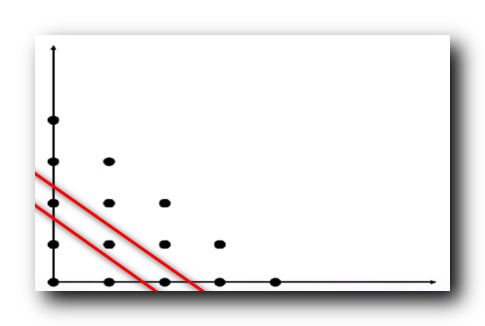
此时在
(
0
,
2
)
,
(
1
,
1
)
,
(
2
,
0
)
(0,2) , (1,1) , (2, 0)
(0,2),(1,1),(2,0) 斜线上的点都为真 , 即上图红框中的点 ;
根据上面斜线上的点可以证明 下一跳斜线上 的点
(
0
,
3
)
,
(
1
,
2
)
,
(
2
,
1
)
,
(
3
,
0
)
(0, 3) , (1, 2) , (2, 1) , (3, 0)
(0,3),(1,2),(2,1),(3,0) 斜线上的点为真 ;
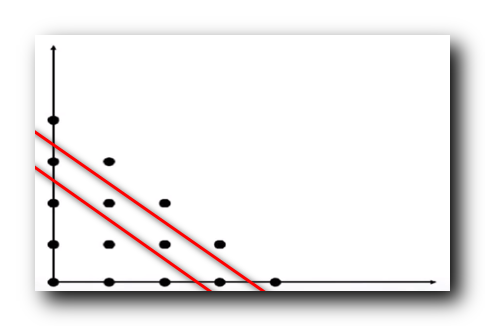
此时证明完毕后 , 上图红框中的点都为真 ;
最终证明所有的斜线 ( 左上角 -> 右下角 ) 上的点都为真 ;
 IDEA激活码
IDEA激活码


