文章目录
- 一、链
- 二、反链
- 三、链与反链示例
- 四、链与反链定理
- 五、链与反链推论
- 六、链与反链推论示例
- 七、良序关系
一、链
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
偏序集中一组元素组成集合
B
B
B , 如果
B
B
B 集合中的元素两两都可比 , 则称
B
B
B 集合是该偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 的链 ;
符号化表示 :
∀
x
∀
y
(
x
∈
B
∧
y
∈
B
→
x
与
y
可
比
)
\forall x \forall y ( x \in B \land y \in B \to x 与 y 可比 )
∀x∀y(x∈B∧y∈B→x与y可比)
链的本质是一个集合
∣
B
∣
|B|
∣B∣ 是链的长度
二、反链
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
偏序集中一组元素组成集合
B
B
B , 如果
B
B
B 集合中的元素两两都 不可比 , 则称
B
B
B 集合是该偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 的 反链 ;
符号化表示 :
∀
x
∀
y
(
x
∈
B
∧
y
∈
B
∧
x
≠
y
→
x
与
y
不
可
比
)
\forall x \forall y ( x \in B \land y \in B \land x\not= y \to x 与 y 不可比 )
∀x∀y(x∈B∧y∈B∧x=y→x与y不可比)
反链的本质是一个集合
∣
B
∣
|B|
∣B∣ 是反链的长度
三、链与反链示例
参考博客 : 【集合论】偏序关系 相关题目解析 ( 偏序关系 中的特殊元素 | 绘制哈斯图 | 链 | 反链 )
四、链与反链定理
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
A
A
A 集合中最长链长度是
n
n
n , 则有以下结论 :
①
A
A
A 集合中存在极大元 ;
A
A
A 集合的极大元就是最长链中最大的元素 ;
②
A
A
A 集合中存在
n
n
n 个划分块 , 每个划分块都是反链 ;
将 链 中的极大元 , 与该极大元不可比的元素放在一个集合中 , 构成一个划分块 ; ( 注意划分块中的元素互相不可比 )
在链上剩余的元素中 , 再次选择一个极大元 , 然后将与该极大元不可比的元素放在一个集合中 , 构成另一个划分块 ;
⋮
\vdots
⋮
下面的示例讲解了如何划分 :
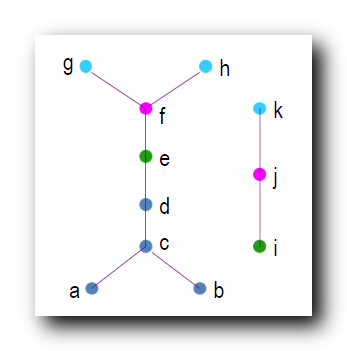
上述偏序集中 , 最长的链长度是
6
6
6 ;
① 将极大元
g
,
h
g,h
g,h , 与该极大元不可比的剩余元素
k
k
k 放在一个集合中 ;
A
1
=
{
g
,
h
,
k
}
A_1 = \{ g , h , k \}
A1={g,h,k}
② 将剩余元素的极大元
f
f
f , 与该极大元不可比的剩余元素
j
j
j 放在一个集合中 ;
A
2
=
{
f
,
j
}
A_2 = \{ f,j \}
A2={f,j}
③ 将剩余元素的极大元
e
e
e , 与该极大元不可比的剩余元素
i
i
i 放在一个集合中 ;
A
3
=
{
e
,
i
}
A_3 = \{ e, i \}
A3={e,i}
④ 将剩余元素的极大元
d
d
d , 剩余的元素都与该极大元科比 ;
A
4
=
{
d
}
A_4 = \{ d \}
A4={d}
⑤ 将剩余元素的极大元
c
c
c , 剩余的元素都与该极大元科比 ;
A
5
=
{
c
}
A_5 = \{ c\}
A5={c}
⑥ 将剩余元素的极大元
a
,
b
a,b
a,b , 没有剩余元素了 ;
A
6
=
{
a
,
b
}
A_6 = \{ a,b \}
A6={a,b}
整体的划分为 :
A
=
{
{
g
,
h
,
k
}
,
{
f
,
j
}
,
{
e
,
i
}
,
{
d
}
,
{
c
}
,
{
a
,
b
}
}
\mathscr{A} = \{ \{ g , h , k \} ,\{ f,j \} , \{ e, i \} , \{ d \} , \{ c\} , \{ a,b \} \}
A={{g,h,k},{f,j},{e,i},{d},{c},{a,b}}
每次都将最长链去掉一层 , 最终将最长链去除干净 , 得到
n
n
n 个划分块 ;
五、链与反链推论
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
A
A
A 集合大小为
m
n
+
1
mn + 1
mn+1 ,
∣
A
∣
=
m
n
+
1
|A| = mn + 1
∣A∣=mn+1 , 则有以下结论 :
A
A
A 集合中要么存在
m
+
1
m+1
m+1 的反链 , 要么存在
n
+
1
n + 1
n+1 的链 ;
使用反证法证明 :
如果既没有
m
+
1
m+1
m+1 的反连 , 又没有
n
+
1
n + 1
n+1 的链 ,
假设有长度为
n
n
n 的链 , 长度为
m
m
m 的反连 ,
A
A
A 集合最多划分
n
n
n 个划分块 , 每个划分块最多有
m
m
m 个元素 , 该集合最多有
m
n
m n
mn 个元素 , 与
∣
A
∣
=
m
n
+
1
|A| = mn + 1
∣A∣=mn+1 矛盾 ;
六、链与反链推论示例

上述偏序集中 , 最长的链长度是
6
6
6 ;
A
=
{
a
,
b
,
c
,
d
,
e
,
f
,
g
,
h
,
k
,
j
,
i
}
A = \{ a,b,c,d,e,f,g,h,k,j,i \}
A={a,b,c,d,e,f,g,h,k,j,i} 集合中 , 元素个数是
11
11
11 个 ,
A
A
A 集合中有
-
长度为
6
6
6 的链 ,
{
a
,
c
,
d
,
e
,
f
,
g
}
\{ a, c,d, e,f, g \}
{a,c,d,e,f,g} ,
{
b
,
c
,
d
,
e
,
f
,
h
}
\{ b, c,d, e,f, h \}
{b,c,d,e,f,h}
-
长度为
3
3
3 的反链 ,
{
g
,
h
,
k
}
\{ g,h,k \}
{g,h,k} ,
{
a
,
b
,
i
}
\{ a,b,i \}
{a,b,i} ,
{
g
,
h
,
i
}
\{ g,h,i \}
{g,h,i} ,
{
a
,
b
,
k
}
\{ a,b,k \}
{a,b,k}
∣
A
∣
=
11
=
2
×
5
+
1
|A| = 11 = 2 \times 5 + 1
∣A∣=11=2×5+1
A
A
A 集合中要么有长度为
2
+
1
=
3
2 + 1 = 3
2+1=3 的反链 , 要么有长度为
5
+
1
=
6
5 + 1 = 6
5+1=6 的链 ; ( 两个都满足 )
或
A
A
A 集合中要么有长度为
5
+
1
=
6
5 + 1 = 6
5+1=6 的反链 , 要么有长度为
2
+
1
=
3
2 + 1 = 3
2+1=3 的链 ; ( 满足长度为
3
3
3 的链 )
A
A
A 集合上的划分 :
-
A
=
{
{
g
,
h
,
k
}
,
{
f
,
j
}
,
{
e
,
i
}
,
{
d
}
,
{
c
}
,
{
a
,
b
}
}
\mathscr{A} = \{ \{ g , h , k \} ,\{ f,j \} , \{ e, i \} , \{ d \} , \{ c\} , \{ a,b \} \}
A={{g,h,k},{f,j},{e,i},{d},{c},{a,b}} -
A
=
{
{
g
,
h
}
,
{
f
}
,
{
e
}
,
{
d
}
,
{
c
,
j
}
,
{
a
,
b
,
i
}
}
\mathscr{A} = \{ \{ g , h \} ,\{ f \} , \{ e \} , \{ d \} , \{ c, j\} , \{ a,b , i \} \}
A={{g,h},{f},{e},{d},{c,j},{a,b,i}}
七、良序关系
<
A
,
≺
>
<A, \prec>
<A,≺> 是 拟全序集 ,
如果
A
A
A 集合中的任何非空子集
B
B
B , 都有最小元 ,
则称
≺
\prec
≺ 是集合
A
A
A 上的良序关系 ,
称
<
A
,
≺
>
<A, \prec>
<A,≺> 为良序集
<
N
,
<
>
<N, <>
<N,<> 是良序集 ,
N
N
N 集合中的非空子集有最小元 , 最小就是
0
0
0 ;
<
Z
,
<
>
<Z, <>
<Z,<> 不是良序集 ,
Z
Z
Z 集合中的非空子集可能没有最小元 , 可能是
−
∞
-\infty
−∞ ;
 IDEA激活码
IDEA激活码


