文章目录
- 一、最大元
- 二、最小元
- 三、最大元、最小元示例
- 四、极大元
- 五、极小元
- 六、极大元、极小元示例
- 七、上界
- 八、下界
- 九、上界、下界示例
- 十、上确界 ( 最小上界 )
- 十一、下确界 ( 最大下界 )
- 十二、上确界、下确界示例
一、最大元
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
B
B
B 中的所有元素与
y
y
y 都是可比的 ,
B
B
B 中的任意元素
x
x
x , 都满足
x
x
x 小于等于
y
y
y
符号化表示 :
∀
x
(
x
∈
B
→
x
≼
y
)
\forall x ( x \in B \to x \preccurlyeq y )
∀x(x∈B→x≼y)
称
y
y
y 是
B
B
B 集合的最大元 ;
二、最小元
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
B
B
B 中的所有元素与
y
y
y 都是可比的 ,
B
B
B 中的任意元素
x
x
x , 都满足
y
y
y 小于等于
x
x
x
符号化表示 :
∀
x
(
x
∈
B
→
y
≼
x
)
\forall x ( x \in B \to y \preccurlyeq x )
∀x(x∈B→y≼x)
称
y
y
y 是
B
B
B 集合的最小元 ;
三、最大元、最小元示例
集合
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={1,2,3,4,5,6,9,10,15} ,
集合
A
A
A 上的整除关系 “
∣
|
∣” 是偏序关系 ,
偏序集是
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x 整除
y
y
y ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
y
y
y 能被
x
x
x 整除 ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
绘制上述偏序集的哈斯图 :
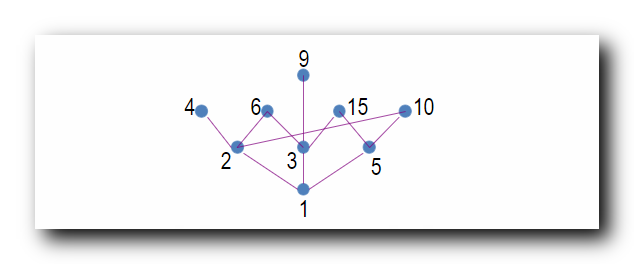
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
B
3
=
A
B_3 = A
B3=A
求上述集合的 最大元 , 最小元 ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
- 最大元 :
2
,
3
2, 3
2,3互相不可比 , 没有最大元 ; - 最小元 :
1
1
1 与其它元素都是可比的 , 都小于等于其它元素 ,1
1
1 是最小元 ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
- 最大元 :
15
15
15 与其它元素都是可比的 , 都大于等于其它元素 ,15
15
15 是最大元 ; - 最小元 :
3
,
5
3, 5
3,5互相不可比 , 没有最小元 ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={1,2,3,4,5,6,9,10,15}
- 最大元 :
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10互相不可比 , 没有最大元 ; - 最小元 :
1
1
1 与其它元素都是可比的 , 都小于等于其它元素 ,1
1
1 是最小元 ;
四、极大元
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
在
B
B
B 中没有比
y
y
y 更大的元素 ,
符号化表示 :
∀
x
(
x
∈
B
∧
y
≼
x
→
x
=
y
)
\forall x ( x \in B \land y \preccurlyeq x \to x = y )
∀x(x∈B∧y≼x→x=y)
称
y
y
y 是
B
B
B 集合的 极大元 ;
五、极小元
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
在
B
B
B 中没有比
y
y
y 更小的元素 ,
符号化表示 :
∀
x
(
x
∈
B
∧
x
≼
y
→
x
=
y
)
\forall x ( x \in B \land x \preccurlyeq y \to x = y )
∀x(x∈B∧x≼y→x=y)
称
y
y
y 是
B
B
B 集合的 极小元 ;
六、极大元、极小元示例
集合
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={1,2,3,4,5,6,9,10,15} ,
集合
A
A
A 上的整除关系 “
∣
|
∣” 是偏序关系 ,
偏序集是
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x 整除
y
y
y ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
y
y
y 能被
x
x
x 整除 ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
绘制上述偏序集的哈斯图 :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
B
3
=
A
B_3 = A
B3=A
求上述集合的 极大元 , 极小元 ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
- 极大元 :
2
,
3
2, 3
2,3互相不可比 , 没有比2
,
3
2,3
2,3 更大的元素 ,2
,
3
2,3
2,3 是极大元 ; - 极小元 :
1
1
1 与其它元素都是可比的 , 都小于等于其它元素 , 没有比1
1
1 更小的元素 ,1
1
1 是极小元 ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
- 极大元 :
15
15
15 与其它元素都是可比的 , 都大于等于其它元素 , 没有比15
15
15 更大的元素 ,15
15
15 是 极大元 ; - 最小元 :
3
,
5
3, 5
3,5互相不可比 , 没有比3
,
5
3,5
3,5 更小的元素 ,3
,
5
3,5
3,5 是极小元 ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={1,2,3,4,5,6,9,10,15}
- 极大元 :
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10互相不可比 , 没有比9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 更大的元素 ,9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 是极大元 ; - 极小元 :
1
1
1 与其它元素都是可比的 , 都小于等于其它元素 , 没有比1
1
1 更小的元素 ,1
1
1 是极小元 ;
七、上界
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
y
y
y 比
B
B
B 中所有的元素都要大
符号化表示 :
∀
x
(
x
∈
B
→
x
≼
y
)
\forall x ( x \in B \to x \preccurlyeq y )
∀x(x∈B→x≼y)
称
y
y
y 是
B
B
B 集合的 上界 ;
八、下界
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
y
y
y 比
B
B
B 中所有的元素都要小
符号化表示 :
∀
x
(
x
∈
B
→
y
≼
x
)
\forall x ( x \in B \to y \preccurlyeq x )
∀x(x∈B→y≼x)
称
y
y
y 是
B
B
B 集合的 下界 ;
九、上界、下界示例
集合
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={1,2,3,4,5,6,9,10,15} ,
集合
A
A
A 上的整除关系 “
∣
|
∣” 是偏序关系 ,
偏序集是
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x 整除
y
y
y ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
y
y
y 能被
x
x
x 整除 ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
绘制上述偏序集的哈斯图 :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
B
3
=
A
B_3 = A
B3=A
求上述集合的 上界 , 下界 ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
- 上界 :
6
6
6 与1
,
2
,
3
1, 2, 3
1,2,3 可比 ,6
6
6 比B
1
B_1
B1 中所有元素都大 ,6
6
6 是上界 ; - 下界 :
1
1
1 与1
,
2
,
3
1, 2, 3
1,2,3 可比 ,1
1
1 比B
1
B_1
B1 中所有元素都小 ,1
1
1 是下界 ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
- 上界 :
15
15
15 与3
,
5
,
15
3 , 5, 15
3,5,15 可比 ,15
15
15 比B
2
B_2
B2 中所有元素都大 ,15
15
15 是上界 ; - 下界 :
1
1
1 与3
,
5
,
15
3 , 5, 15
3,5,15 可比 ,1
1
1 比B
2
B_2
B2 中所有元素都小 ,1
1
1 是下界 ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={1,2,3,4,5,6,9,10,15}
- 上界 : 不存在元素与
B
3
B_3
B3 中的元素都可比 ; 不存在上界 ; - 下界 :
1
1
1 与B
3
B_3
B3 中的元素可比 ,1
1
1 比B
3
B_3
B3 中所有元素都小 ,1
1
1 是下界 ;
十、上确界 ( 最小上界 )
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
上界中最小的元素就是 最小上界, 又称为上确界
十一、下确界 ( 最大下界 )
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> 是 偏序集 ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
下界中最大的元素就是 最大下界, 又称为下确界
十二、上确界、下确界示例
集合
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={1,2,3,4,5,6,9,10,15} ,
集合
A
A
A 上的整除关系 “
∣
|
∣” 是偏序关系 ,
偏序集是
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x 整除
y
y
y ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
y
y
y 能被
x
x
x 整除 ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
绘制上述偏序集的哈斯图 :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
B
3
=
A
B_3 = A
B3=A
求上述集合的 上确界( 最小上界 ) , 下确界 ( 最大下界 ) ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={1,2,3}
- 上确界 :
6
6
6 与1
,
2
,
3
1, 2, 3
1,2,3 可比 ,6
6
6 比B
1
B_1
B1 中所有元素都大 ,6
6
6 是上界 ;6
6
6 也是上确界 , 最小上界 ; - 下确界 :
1
1
1 与1
,
2
,
3
1, 2, 3
1,2,3 可比 ,1
1
1 比B
1
B_1
B1 中所有元素都小 ,1
1
1 是下界 ;1
1
1 也是下确界 , 最大下界 ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={3,5,15}
- 上确界 :
15
15
15 与3
,
5
,
15
3 , 5, 15
3,5,15 可比 ,15
15
15 比B
2
B_2
B2 中所有元素都大 ,15
15
15 是上界 ;15
15
15 也是上确界 , 最小上界 ; - 下确界 :
1
1
1 与3
,
5
,
15
3 , 5, 15
3,5,15 可比 ,1
1
1 比B
2
B_2
B2 中所有元素都小 ,1
1
1 是下界 ;1
1
1 也是下确界 , 最大下界 ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={1,2,3,4,5,6,9,10,15}
- 上确界 : 不存在元素与
B
3
B_3
B3 中的元素都可比 ; 不存在上界 ; 不存在 上确界 / 最小上界 ; - 下确界 :
1
1
1 与B
3
B_3
B3 中的元素可比 ,1
1
1 比B
3
B_3
B3 中所有元素都小 ,1
1
1 是下界 ;1
1
1 也是下确界 , 最大下界 ;
 IDEA激活码
IDEA激活码


