一、全序关系 ( 线序关系 )

---

A

A

A 集合与该集合之上的 偏序关系

≼

\preccurlyeq

≼ 组成的有序对是 :

<

A

,

≼

>

<A, \preccurlyeq>

<A,≼> 偏序集 ;

A

A

A 集合中 任意元素

x

,

y

x, y

x,y 都 可比 ;

则称

≼

\preccurlyeq

≼ 关系是

A

A

A 集合上的 全序关系, 又称为 线序关系 ;

称

<

A

,

≼

>

<A, \preccurlyeq>

<A,≼> 为全序集 ( 线序集 ) ;

<

A

,

≼

>

<A, \preccurlyeq>

<A,≼> 偏序集 是全序集

当且仅当

<

A

,

≼

>

<A, \preccurlyeq>

<A,≼> 偏序集的哈斯图是一条直线

二、全序关系示例

---

非空集合

A

A

A 包含于 实数集

R

R

R ,

∅

≠

A

⊆

R

\varnothing \not= A \subseteq R

∅​=A⊆R ,

A

A

A 集合上的 大于等于

≥

\geq

≥ , 小于等于

≤

\leq

≤ 都是

A

A

A 集合上的 全序关系 ,

<

A

,

≤

>

<A , \leq>

<A,≤> ,

<

A

,

≥

>

<A , \geq>

<A,≥> 是 全序集 ;

哈斯图是一条直线 ;

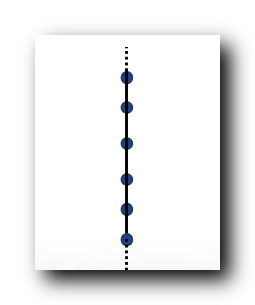
三、拟序关系

---

非空集合

A

A

A , 二元关系

R

R

R 是

A

A

A 集合上的二元关系 ;

符号化表示 :

A

≠

∅

A \not= \varnothing

A​=∅ ,

R

⊆

A

×

A

R \subseteq A \times A

R⊆A×A ;

如果 二元关系

R

R

R 是 反自反 , 传递 的 ,

则称

R

R

R 关系是

A

A

A 集合上的拟序关系 ,

使用

≺

\prec

≺ 表示拟序关系 ,

称

<

A

,

≺

>

<A , \prec>

<A,≺> 是拟序集 ;

偏序关系

≼

\preccurlyeq

≼ 是 小于等于 关系 , 拟序关系

≺

\prec

≺ 就是 严格小于 关系 ;

拟序关系示例 : 大于 , 小于 , 真包含 , 都是拟序关系 ;

拟序关系 完整的性质是 反自反 , 反对称 , 传递 ,
之所以概念中没有提 反对称 性质 , 是因为 根据 反自反 , 传递性质 , 可以推导出 反对称 性质 ;

数学中倾向于使用最小的条件进行定义 , 因此这里将反对称性去掉 ;

四、拟序关系定理 1

---

非空集合

A

A

A ,

A

≠

∅

A \not= \varnothing

A​=∅ ,

≼

\preccurlyeq

≼ 是非空集合

A

A

A 上的偏序关系 ,

≺

\prec

≺ 是非空集合

A

A

A 上的拟序关系 ;

① 偏序关系性质 :

≼

\preccurlyeq

≼ 是 自反 , 反对称 , 传递的

② 拟序关系性质 :

≺

\prec

≺ 是 反自反 , 反对称 , 传递的

③ 偏序关系 -> 拟序关系 : 偏序关系 减去 恒等关系 就是 拟序关系 ,

≼

−

I

A

=

≺

\preccurlyeq - I_A = \prec

≼−IA​=≺

④ 拟序关系 -> 偏序关系 : 拟序关系 与 恒等关系 的并集就是 偏序关系 ,

≺

∪

I

A

=

≼

\prec \cup I_A = \preccurlyeq

≺∪IA​=≼ ;

四、拟序关系定理 2

---

非空集合

A

A

A ,

A

≠

∅

A \not= \varnothing

A​=∅ ,

≺

\prec

≺ 是非空集合

A

A

A 上的拟序关系 ;

①

x

≺

y

x \prec y

x≺y ,

x

=

y

x=y

x=y ,

y

≺

x

y \prec x

y≺x 中最多有一个成立 ;

使用反证法 , 任意两个成立都会导致

x

≺

x

x \prec x

x≺x ;

②

(

x

≺

y

∧

x

=

y

)

∧

(

y

≺

x

∧

x

=

y

)

⇒

x

=

y

(x\prec y \land x = y) \land (y \prec x \land x=y) \Rightarrow x = y

(x≺y∧x=y)∧(y≺x∧x=y)⇒x=y

五、三歧性、拟线序

---

非空集合

A

A

A ,

A

≠

∅

A \not= \varnothing

A​=∅ ,

≺

\prec

≺ 是非空集合

A

A

A 上的拟序关系 ;

如果

x

≺

y

x \prec y

x≺y ,

x

=

y

x=y

x=y ,

y

≺

x

y \prec x

y≺x 中仅有一个城里 , 那么称

≺

\prec

≺ 拟序关系 具有 三歧性 ;

有三歧性的 逆序关系

≺

\prec

≺ 称为

A

A

A 集合上的 拟线序关系 , 又称为拟全序关系 ;

<

A

≺

>

<A \prec>

<A≺> 被称为 拟线序集 ;