文章目录
- 一、哈斯图示例 ( 整除关系 )
- 二、哈斯图示例 ( 包含关系 )
- 三、哈斯图示例 ( 加细关系 )
一、哈斯图示例 ( 整除关系 )
集合
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={1,2,3,4,5,6,9,10,15} ,
集合
A
A
A 上的整除关系 “
∣
|
∣” 是偏序关系 ,
偏序集是
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x 整除
y
y
y ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
y
y
y 能被
x
x
x 整除 ,
x
x
x 是除数 (分母) ,
y
y
y 是被除数 (分子) ;
y
x
\dfrac{y}{x}
xy
绘制上述偏序集的哈斯图 :
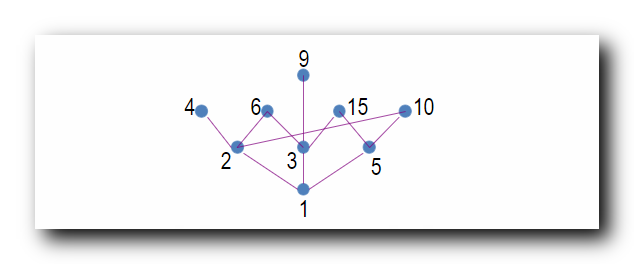
1
1
1 是最小的 ,
1
1
1 能整除所有的数 ;
1
1
1 上面的一层是素数 , 素数只能被
1
1
1 和其本身整除 ; 素数肯定是覆盖
1
1
1 的 ; 即素数与
1
1
1 之间没有元素 ;
素数之上的数 , 由素数相乘的数组成 ;
6
6
6 既可以整除
2
2
2 , 又可以整除
3
3
3 , 因此其既覆盖
2
2
2 , 又覆盖
3
3
3 ;
10
10
10 既可以整除
2
2
2 , 又可以整除
5
5
5 , 因此其既覆盖
2
2
2 , 又覆盖
5
5
5 ;
15
15
15 既可以整除
3
3
3 , 又可以整除
5
5
5 , 因此其既覆盖
3
3
3 , 又覆盖
5
5
5 ;
4
4
4 可以整除
2
2
2 , 因此
4
4
4 覆盖
2
2
2 ;
9
9
9 可以整除
3
3
3 , 因此
9
9
9 覆盖
3
3
3 ;
二、哈斯图示例 ( 包含关系 )
集合
A
=
{
a
,
b
,
c
}
A = \{ a, b , c \}
A={a,b,c} ,
集族
A
\mathscr{A}
A 包含于
A
A
A 集合的幂集 ,
A
⊆
P
(
A
)
\mathscr{A} \subseteq P(A)
A⊆P(A) ,
集族
A
=
{
∅
,
{
a
}
,
{
b
}
,
{
c
}
,
{
a
,
b
}
,
{
b
,
c
}
,
{
a
,
c
}
}
\mathscr{A} = \{ \varnothing , \{ a \} , \{ b \} , \{ c \} , \{ a , b \} , \{ b,c \} , \{ a, c \} \}
A={∅,{a},{b},{c},{a,b},{b,c},{a,c}}
集族
A
\mathscr{A}
A 上的 包含关系 “
⊆
\subseteq
⊆” 是偏序关系 ,
偏序集是
<
A
,
⊆
>
<\mathscr{A} , \subseteq >
<A,⊆>
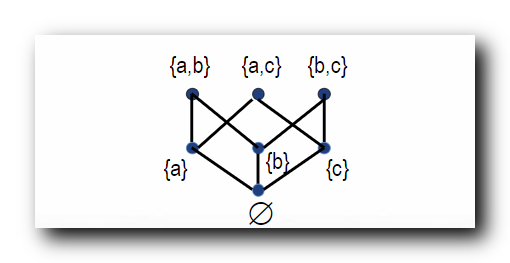
空集 包含于 所有集合 , 是最小的 , 在哈斯图最下面 ;
空集 之上是单元集 , 单元集 覆盖 空集 , 它们之间并不会有第三个元素 ;
三个单元集之间相互没有包含关系 , 是不可比的 ;
单元集 之上是 双元集 , 每个 双元集 之下就是其包含的对应的单元集 ;
三、哈斯图示例 ( 加细关系 )
加细关系 是 有序对集合 , 其中每个 有序对的元素 是 集族 ;
集合
A
A
A 非空 ,
π
\pi
π 是
A
A
A 集合划分组成的集合 , 每个划分都是一个集族 ;
划分参考 : 【集合论】划分 ( 划分 | 划分示例 | 划分与等价关系 )
集族之间有一种关系 , 加细关系 , 使用符号
≼
加
细
\preccurlyeq_{加细}
≼加细 表示 ;
加细关系
≼
加
细
\preccurlyeq_{加细}
≼加细 符号化表示 :
≼
加
细
=
{
<
x
,
y
>
∣
x
,
y
∈
π
∧
x
是
y
的
加
细
}
\preccurlyeq_{加细} = \{ <x, y> | x, y \in \pi \land x 是 y 的加细 \}
≼加细={<x,y>∣x,y∈π∧x是y的加细}
前提 :
-
集合
A
=
{
a
,
b
,
c
,
d
}
A = \{ a, b , c , d \}
A={a,b,c,d}
-
集族
A
1
=
{
{
a
}
,
{
b
}
,
{
c
}
,
{
d
}
}
\mathscr{A}_1= \{ \{ a \} , \{ b \} , \{ c \} , \{ d \} \}
A1={{a},{b},{c},{d}}
-
集族
A
2
=
{
{
a
,
b
}
,
{
c
,
d
}
}
\mathscr{A}_2 = \{ \{ a , b \} , \{ c , d \} \}
A2={{a,b},{c,d}}
-
集族
A
3
=
{
{
a
,
c
}
,
{
b
,
d
}
}
\mathscr{A}_3= \{ \{ a,c \} , \{ b,d\} \}
A3={{a,c},{b,d}}
-
集族
A
4
=
{
{
a
}
,
{
b
,
c
,
d
}
}
\mathscr{A}_4= \{ \{ a \} , \{ b, c , d \} \}
A4={{a},{b,c,d}}
-
集族
A
5
=
{
{
a
}
,
{
b
}
,
{
c
,
d
}
}
\mathscr{A}_5= \{ \{ a \} , \{ b \} , \{ c , d \} \}
A5={{a},{b},{c,d}}
-
集族
A
6
=
{
{
a
,
b
,
c
,
d
}
}
\mathscr{A}_6 = \{ \{ a , b , c , d\} \}
A6={{a,b,c,d}}
上述集族都是
A
A
A 集合的划分 ;
划分关系的哈斯图 :
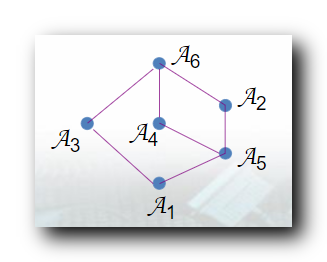
A
1
\mathscr{A}_1
A1 是所有划分的加细 , 是最细的划分 , 在哈斯图最下面 ;
所有的划分都是
A
6
\mathscr{A}_6
A6 的加细 , 是最粗粒度的划分, 在哈斯图最上面 ;
A
5
\mathscr{A}_5
A5 既是
A
2
\mathscr{A}_2
A2 的加细 , 又是
A
4
\mathscr{A}_4
A4 的加细 ;
A
3
\mathscr{A}_3
A3 与
A
4
\mathscr{A}_4
A4 互相不是对方的加细 , 不可比 ;
A
2
\mathscr{A}_2
A2 与
A
4
\mathscr{A}_4
A4 互相不是对方的加细 , 不可比 ;
A
2
\mathscr{A}_2
A2 与
A
3
\mathscr{A}_3
A3 互相不是对方的加细 , 不可比 ;
A
3
\mathscr{A}_3
A3 与
A
5
\mathscr{A}_5
A5 互相不是对方的加细 , 不可比 ;
 IDEA激活码
IDEA激活码


