文章目录
- 一、可比
- 二、严格小于
- 三、覆盖
- 四、哈斯图
一、可比
可比 :
A
A
A 集合 , 该集合上存在 偏序关系
≼
\preccurlyeq
≼ 小于等于 ,
偏序集 是 集合 和 偏序关系 组成的有序对
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
要么是
x
≼
y
x \preccurlyeq y
x≼y , 要么就是
y
≼
x
y \preccurlyeq x
y≼x , 符号化表示是
x
≼
y
∨
y
≼
x
x \preccurlyeq y \lor y \preccurlyeq x
x≼y∨y≼x , 两种情况必选其一 ,
则称
x
x
x 与
y
y
y 是可比的 ;
只要
x
,
y
x, y
x,y 之间 存在偏序关系 , 不管谁在前 , 谁在后 , 都 统一称
x
x
x 与
y
y
y 是可比的 ;
二、严格小于
严格小于 概念需要基于 可比概念
严格小于 :
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
如果
x
,
y
x , y
x,y 是可比的 (
x
,
y
x,y
x,y 之间存在偏序关系 ) , 但是
x
x
x 与
y
y
y 不相等 , 则称
x
x
x 严格小于
y
y
y ;
符号化表示 :
x
≼
y
∧
x
≠
y
⇔
x
≺
y
x \preccurlyeq y \land x \not= y \Leftrightarrow x \prec y
x≼y∧x=y⇔x≺y
三、覆盖
覆盖 概念需要基于 严格小于概念
覆盖 :
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
,
z
x, y , z
x,y,z 是
A
A
A 集合中的元素 ,
x
,
y
,
z
∈
A
x , y , z \in A
x,y,z∈A ,
x
x
x 严格小于
y
y
y ,
x
≺
y
x \prec y
x≺y ,
不存在
z
z
z , 使
x
x
x 严格小于
z
z
z , 并且
z
z
z 严格小于
y
y
y ,
则称
y
y
y 覆盖
x
x
x ; ( 注意是 大 覆盖 小 )
偏序关系中 大 覆盖 小
符号化表示 :
x
≺
y
∧
¬
∃
z
(
z
∈
A
∧
x
≺
y
≺
z
)
x \prec y \land \lnot \exist z( z \in A \land x \prec y \prec z )
x≺y∧¬∃z(z∈A∧x≺y≺z)
四、哈斯图
A
A
A 集合 与
A
A
A 上偏序关系
≼
\preccurlyeq
≼ , 组成 偏序集
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> ,
x
,
y
x, y
x,y 是
A
A
A 集合中的两个元素 ,
x
,
y
∈
A
x , y \in A
x,y∈A ,
哈斯图 :
① 顶点 : 使用 顶点 表示
A
A
A 集合中的元素 ;
② 无向边 : 当且仅当
y
y
y 覆盖
x
x
x 时 ,
y
y
y 顶点在
x
x
x 顶点 上方 , 并且在
x
x
x 顶点 与
y
y
y 顶点之间 绘制一条 无向边 ;
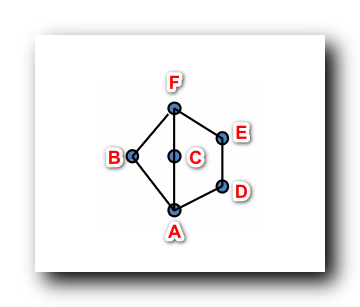
上图是
6
6
6 元集 上的偏序关系
≼
\preccurlyeq
≼
A
A
A 元素比
B
,
C
,
D
B,C,D
B,C,D 元素都小
偏序关系是传递的 ,
A
A
A 比
B
B
B 小 ,
B
B
B 比
F
F
F 小 , 因此
A
A
A 比
F
F
F 小
最下面的元素
A
A
A 是最小的 , 所有的元素都比
A
A
A 大 ( 包括
A
A
A , 偏序关系是自反的 )
最上面的元素
F
F
F 是最大的 , 所有的元素都比
F
F
F 小 ( 包括
F
F
F , 偏序关系是自反的 )
B
C
D
E
BCDE
BCDE 四个元素互相都不可比
哈斯图 与 关系图对比 省略的内容 :
① 环 : 偏序关系是自反的 , 因此 每个顶点上都有环 , 可以省略掉环
② 箭头 : 偏序关系是反对称的 , 因此 两个顶点两两之间肯定没有双向边 , 都是单向边 , 因此可以省略箭头方向
③ 默认方向 : 使用上下位置表示箭头的方向 , 箭头默认向上 , 偏序是 小于等于 , 最小的在最小面, 最大的在最上面 ;
 IDEA激活码
IDEA激活码


