文章目录
- 一、划分
- 二、划分示例
- 三、划分与等价关系定理
一、划分
划分 :
非空集合
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
A
A
A 集合的一个 划分 是 集族
A
\mathscr{A}
A ,
该 集族
A
\mathscr{A}
A 包含于
A
A
A 集合的幂集 ,
A
⊆
P
(
A
)
\mathscr{A} \subseteq P(A)
A⊆P(A) , 集族中的元素都属于
A
A
A 集合的幂集 ;
集族
A
\mathscr{A}
A 中的元素是 集合 , 称为 划分块 ( Block ) , 集合中的元素都是
A
A
A 集合中的元素 ;
该集族
A
\mathscr{A}
A 有以下性质 :
①
A
\mathscr{A}
A 集族中每个元素都非空
∅
∉
A
\varnothing \not\in \mathscr{A}
∅∈A
②
A
\mathscr{A}
A 集族中任意两个元素 ( 划分块 / 集合 ) 是不相交的
∀
x
,
y
(
x
,
y
∈
A
∧
x
≠
y
⇒
x
∩
y
=
∅
)
\forall x,y ( x,y \in \mathscr{A} \land x \not= y \Rightarrow x \cap y = \varnothing )
∀x,y(x,y∈A∧x=y⇒x∩y=∅)
③
A
\mathscr{A}
A 集族中所有的元素 ( 划分块 / 集合 ) 的并集是
A
A
A 集合
⋃
A
=
A
\bigcup \mathscr{A} = A
⋃A=A
商集就是一个划分 , 该集族中的元素是等价类集合 ;
商集参考 : 【集合论】等价类 ( 等价类概念 | 等价类示例 | 等价类性质 | 商集 | 商集示例 ) 四、商集
二、划分示例
全集是
E
E
E ,
取
E
E
E 的
n
n
n 个 非平凡 的 真子集 , 非平凡的含义是既不是空集 , 也不是它自己 ;
∅
≠
A
1
,
A
2
,
⋯
,
A
n
⊂
E
\varnothing \not= A_1 , A_2, \cdots, A_n \subset E
∅=A1,A2,⋯,An⊂E
1. 划分 1 基于
1
1
1 个元素
集族
A
i
=
{
A
i
,
∼
A
i
}
\mathscr{A}_i = \{ A_i , \sim A_i \}
Ai={Ai,∼Ai} ,
i
=
1
,
2
,
⋯
,
n
i = 1, 2, \cdots , n
i=1,2,⋯,n ,
A
i
\mathscr{A}_i
Ai 集族中包含
A
i
A_i
Ai 集合及其补集
∼
A
i
\sim A_i
∼Ai , 该集族
A
i
\mathscr{A}_i
Ai 满足上述划分的三个性质 , 是一个划分 ;
2. 划分 2基于
2
2
2 个元素
集族
A
i
=
{
A
i
∩
A
j
,
∼
A
i
∩
A
j
,
A
i
∩
∼
A
j
,
∼
A
i
∩
∼
A
j
}
−
{
∅
}
\mathscr{A}_i = \{ A_i \cap A_j , \sim A_i \cap A_j , A_i \cap \sim A_j , \sim A_i \cap \sim A_j\} - \{ \varnothing \}
Ai={Ai∩Aj,∼Ai∩Aj,Ai∩∼Aj,∼Ai∩∼Aj}−{∅} ,
i
,
j
=
1
,
2
,
⋯
,
n
∧
i
≠
j
i,j = 1, 2, \cdots , n \land i \not= j
i,j=1,2,⋯,n∧i=j
根据如下文氏图进行理解 :
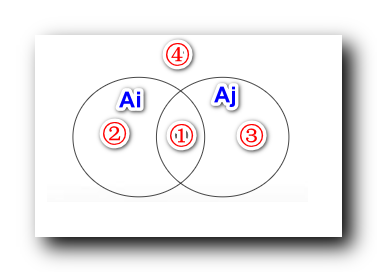
-
A
i
∩
A
j
A_i \cap A_j
Ai∩Aj 对应区域 ① -
∼
A
i
∩
A
j
\sim A_i \cap A_j
∼Ai∩Aj 对应区域 ③ -
A
i
∩
∼
A
j
A_i \cap \sim A_j
Ai∩∼Aj 对应区域 ② -
∼
A
i
∩
∼
A
j
\sim A_i \cap \sim A_j
∼Ai∩∼Aj 对应区域 ④ - 如果
A
i
A_i
Ai 与A
j
A_j
Aj 不相交 , 那么区域 ① 就是空集 , 划分类不能是空集 , 此时就需要减去空集 , 对应−
{
∅
}
-\{ \varnothing \}
−{∅}
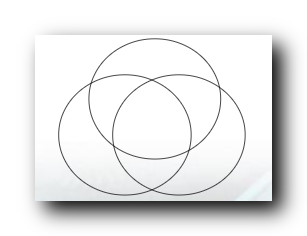
3. 划分 3 基于
3
3
3 个元素
集族
A
i
j
k
=
{
A
i
∩
A
j
∩
A
k
,
A
i
∩
∼
A
j
∩
∼
A
k
,
∼
A
i
∩
A
j
∩
∼
A
k
,
∼
A
i
∩
∼
A
j
∩
A
k
,
∼
A
i
∩
∼
A
j
∩
∼
A
k
}
−
{
∅
}
\mathscr{A}_{ijk} = \{ A_i \cap A_j \cap A_k , A_i \cap \sim A_j \cap \sim A_k , \sim A_i \cap A_j \cap \sim A_k , \sim A_i \cap \sim A_j \cap A_k , \sim A_i \cap \sim A_j \cap \sim A_k\} - \{ \varnothing \}
Aijk={Ai∩Aj∩Ak,Ai∩∼Aj∩∼Ak,∼Ai∩Aj∩∼Ak,∼Ai∩∼Aj∩Ak,∼Ai∩∼Aj∩∼Ak}−{∅}
4. 划分 4 基于
n
n
n 个元素
集族
A
1
,
2
,
⋯
,
n
=
{
A
1
∩
A
2
∩
⋯
∩
A
n
,
A
1
∩
∼
A
2
∩
⋯
∩
∼
A
n
,
∼
A
1
∩
A
2
∩
⋯
∩
∼
A
n
,
⋮
∼
A
1
∩
∼
A
2
∩
⋯
∩
∼
A
n
}
−
{
∅
}
\begin{array}{lcl} \mathscr{A}_{1,2,\cdots,n} = \{ \\\\ A_1\cap A_2 \cap \cdots \cap A_n , \\\\ A_1\cap \sim A_2 \cap \cdots \cap \sim A_n , \\\\ \sim A_1\cap A_2 \cap \cdots \cap \sim A_n , \\\\ \vdots \\\\ \sim A_1\cap \sim A_2 \cap \cdots \cap \sim A_n \\\\ \} - \{ \varnothing \} \end{array}
A1,2,⋯,n={A1∩A2∩⋯∩An,A1∩∼A2∩⋯∩∼An,∼A1∩A2∩⋯∩∼An,⋮∼A1∩∼A2∩⋯∩∼An}−{∅}
规则 :
A
1
A_1
A1 到
A
n
A_n
An 的并集 ,
n
n
n 个
∼
A
1
\sim A_1
∼A1 到
∼
A
n
\sim A_n
∼An 的并集 , 其中每个并集中 , 只有一个不是补集 ,
∼
A
1
\sim A_1
∼A1 到
∼
A
n
\sim A_n
∼An 的并集 ;
三、划分与等价关系定理
划分与等价关系定理 :
前提 : 集合
A
A
A 非空 ,
A
≠
∅
A \not= \varnothing
A=∅
R
R
R 关系是
A
A
A 集合上的等价关系 , 可以推导出 ,
A
A
A 集合关于
R
R
R 关系的商集
A
/
R
A/R
A/R 是
A
A
A 的划分 ;
R
是
A
上
等
价
关
系
⇒
A
/
R
是
A
的
划
分
R 是 A 上等价关系 \Rightarrow A/R 是 A 的划分
R是A上等价关系⇒A/R是A的划分
集族
A
\mathscr{A}
A 是
A
A
A 集合上的划分 , 定义一个 二元关系 是 同块关系
R
A
R_{\mathscr{A}}
RA ,
该 同块关系 是
A
A
A 集合上的 等价关系 ,
该 同块关系 是 由划分
A
\mathscr{A}
A 定义的关系 ;
x
R
A
y
⇔
∃
z
(
z
∈
A
∧
x
∈
z
∧
y
∈
z
)
xR_{\mathscr{A}}y \Leftrightarrow \exist z ( z \in \mathscr{A} \land x \in z \land y \in z )
xRAy⇔∃z(z∈A∧x∈z∧y∈z)
 IDEA激活码
IDEA激活码


