文章目录
- 一、闭包求法
- 二、求闭包示例 ( 关系图角度 )
- 三、求闭包示例 ( 关系矩阵角度 )
- 四、闭包运算与关系性质
- 五、闭包复合运算
一、闭包求法
R
R
R 关系是
A
A
A 集合上的二元关系 ,
R
⊆
A
R \subseteq A
R⊆A , 且
A
A
A 集合不为空集 ,
A
≠
∅
A \not= \varnothing
A=∅
求自反闭包 :
r
(
R
)
=
R
∪
I
A
r(R) = R \cup I_A
r(R)=R∪IA , 给每个顶点添加环 ;
- 如果
R
R
R 关系是自反的 , 当且仅当 ,I
A
⊆
R
I_A \subseteq R
IA⊆R
求对称闭包 :
s
(
R
)
=
R
∪
R
−
1
s(R) = R \cup R^{-1}
s(R)=R∪R−1
- 原来 没有有向边 ( 有序对 ) , 自然也没有对应的逆 , 此时不添加边
- 原来 有一条有向边 ( 有序对 ) , 再添加一个反向的有向边 , 组成 关系图中的 顶点间的 双向有向边
- 原来 有两条有向边 ( 有序对 ) , 此时就不用添加其它边
- 如果
R
R
R 关系是对称的 , 当且仅当 ,R
=
R
−
1
R = R^{-1}
R=R−1
求传递闭包 :
t
(
R
)
=
R
∪
R
2
∪
R
3
∪
⋯
t(R) = R \cup R^2 \cup R^3 \cup \cdots
t(R)=R∪R2∪R3∪⋯
将
R
R
R 关系所有的幂运算值并起来 , 就是其传递闭包 ,
R
R
R 关系的
1
1
1 次幂 ,
R
R
R 关系的
2
2
2 次幂 ,
R
R
R 关系的
3
3
3 次幂 ,
⋯
\cdots
⋯ ,
R
R
R 关系的
n
n
n 次幂 , 并起来 , 就是其传递闭包 ;
如果
A
A
A 是有穷集 , 其关系也是有穷的 , 求出其所有的
n
n
n 次幂 , 不用求出很多幂运算 , 因为关系的幂运算后面都是循环的 , 求出已知的所有
n
n
n 次幂 取 并集即可 ;
如果
R
R
R 关系是传递的 , 当且仅当 ,
R
2
⊆
R
R^2 \subseteq R
R2⊆R
二、求闭包示例 ( 关系图角度 )
集合
A
=
{
a
,
b
,
c
,
d
}
A = \{ a, b, c , d \}
A={a,b,c,d}
关系
R
=
{
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
,
<
c
,
d
>
}
R = \{ <a,b> , <b,a> , <b,c> , <c,d> \}
R={<a,b>,<b,a>,<b,c>,<c,d>}
求关系
R
R
R 的自反闭包
r
(
R
)
r(R)
r(R) , 对称闭包
s
(
R
)
s(R)
s(R) , 传递闭包
t
(
R
)
t(R)
t(R)

求自反闭包 : 就是给每个顶点加上环 :
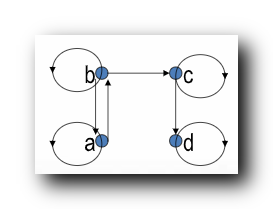
求对称闭包 : 将 顶点间 单向边改成双向边 , 不管 顶点间双向边 和 顶点间没有边 的情况 ;
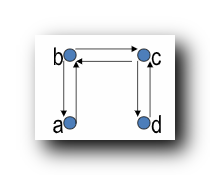
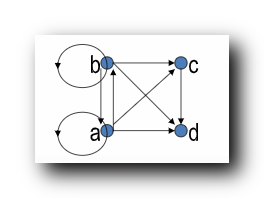
求传递闭包 : 将能到的点直接连起来 ;
- a 可以到 b , 路径 a -> b ; a 可以到 c , 路径是 a -> b -> c ; a 可以到 d , 路径是 a -> b -> c -> d ; 因此添加 a 到 c , d 的有向边 ;
- b 可以到 a , 路径 b -> a ; b 可以到 c , 路径是 b -> c ; b 可以到 d , 路径是 b -> c -> d ; 因此添加 b 到 d 的有向边 ;
- c 可以到 d , 路径 c -> d ; 没有可连接的边 ;
- d 哪都到不了 , 没有可连接的边 ;
- 另外出现双向边时 , 两个顶点必须加环 ;
三、求闭包示例 ( 关系矩阵角度 )
关系
R
=
{
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
,
<
c
,
d
>
}
R = \{ <a, b> , <b,a> , <b,c> , <c,d> \}
R={<a,b>,<b,a>,<b,c>,<c,d>}
使用关系矩阵方法求其 自反闭包 , 对称闭包 , 传递闭包 ;
将上述关系写成矩阵形式为 :
M
(
R
)
=
[
0
1
0
0
1
0
1
0
0
0
0
1
0
0
0
0
]
M(R) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}
M(R)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001000010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
自反闭包 : 将主对角线值 , 全部改成
1
1
1 , 左上角到右下角为主对角线 ;
M
(
r
(
R
)
)
=
[
1
1
0
0
1
1
1
0
0
0
1
1
0
0
0
1
]
M(r(R)) = \begin{bmatrix} 1 & 1 & 0 & 0 \\\\ 1 & 1 & 1 & 0 \\\\ 0 & 0 & 1 & 1 \\\\ 0 & 0 & 0 & 1 \end{bmatrix}
M(r(R))=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1100110001100011⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
对称闭包 : 主对角线两端要对称 , 以对角线为基准 , 使对角线两边的值对称 ;
M
(
s
(
R
)
)
=
[
0
1
0
0
1
0
1
0
0
1
0
1
0
0
1
0
]
M(s(R)) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 1 & 0 \end{bmatrix}
M(s(R))=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100101001010010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
传递闭包 : 求该关系矩阵的 二次幂 , 三次幂 , 四次幂 ,
⋯
\cdots
⋯ , 直到出现相同的循环的值为止 ;
将上述所有的不同的 矩阵幂运算 进行逻辑相加 ( 或 ) 操作 , 就是其传递闭包对应的矩阵 , 计算机算法适合使用该方法 , 如果人计算 , 还是关系图比较形象 ;
参考 : 【集合论】关系表示 ( 关系矩阵 | 关系矩阵示例 | 关系矩阵性质 | 关系矩阵运算 | 关系图 | 关系图示例 | 关系表示相关性质 ) 四、关系矩阵运算
注意逆序合成
M
(
R
2
)
=
M
(
R
∘
R
)
=
M
(
R
)
∙
M
(
R
)
=
[
0
1
0
0
1
0
1
0
0
0
0
1
0
0
0
0
]
∙
[
0
1
0
0
1
0
1
0
0
0
0
1
0
0
0
0
]
=
[
1
0
1
0
0
1
0
1
0
0
0
0
0
0
0
0
]
M(R^2) = M(R \circ R) = M(R) \bullet M(R) =\begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}
M(R2)=M(R∘R)=M(R)∙M(R)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001000010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤∙⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001000010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1000010010000100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
M
(
R
3
)
=
M
(
R
2
∘
R
)
=
M
(
R
)
∙
M
(
R
2
)
=
[
0
1
0
0
1
0
1
0
0
0
0
1
0
0
0
0
]
∙
[
1
0
1
0
0
1
0
1
0
0
0
0
0
0
0
0
]
=
[
0
1
0
1
1
0
1
0
0
0
0
0
0
0
0
0
]
M(R^3) = M(R^2 \circ R) = M(R) \bullet M(R^2) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 1 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}
M(R3)=M(R2∘R)=M(R)∙M(R2)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001000010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤∙⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1000010010000100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001001000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
M
(
R
4
)
=
M
(
R
3
∘
R
)
=
M
(
R
)
∙
M
(
R
3
)
=
[
0
1
0
0
1
0
1
0
0
0
0
1
0
0
0
0
]
∙
[
0
1
0
1
1
0
1
0
0
0
0
0
0
0
0
0
]
=
[
1
0
1
0
0
1
0
1
0
0
0
0
0
0
0
0
]
=
M
(
R
2
)
M(R^4) = M(R^3 \circ R) = M(R) \bullet M(R^3) =\begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 0 & 1 & 0 & 1 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = M(R^2)
M(R4)=M(R3∘R)=M(R)∙M(R3)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001000010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤∙⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0100100001001000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1000010010000100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=M(R2)
因此其
R
4
R^4
R4 之后的幂运算值 , 偶数次幂关系矩阵与
M
(
R
2
)
M(R^2)
M(R2) 值相同 , 奇数次幂关系矩阵与
M
(
R
3
)
M(R^3)
M(R3) 值相同 ;
M
(
t
(
R
)
)
=
M
(
R
)
∨
M
(
R
2
)
∨
M
(
R
3
)
=
[
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
]
M(t(R)) = M(R) \lor M(R^2) \lor M(R^3) =\begin{bmatrix} 1 & 1 & 1 & 1 \\\\ 1 & 1 & 1 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}
M(t(R))=M(R)∨M(R2)∨M(R3)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1100110011001100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
四、闭包运算与关系性质
| 自反性 | 对称性 | 传递性 | |
|---|---|---|---|
|
r ( R ) r(R) r(R) |
1 1 1 ( 本身性质 ) |
1 1 1 |
1 1 1 |
|
r ( R ) r(R) r(R) |
1 1 1 |
1 1 1 ( 本身性质 ) |
|
|
r ( R ) r(R) r(R) |
1 1 1 |
1 1 1 |
1 1 1 ( 本身性质 ) |
上述表格中值为
1
1
1 , 说明原来存在该性质 , 求对应的 自反/对称/传递 闭包后 , 仍具有该性质 , 反之不具有该性质 ;
表格第二行含义 :
r
(
R
)
r(R)
r(R) 对应的行 ;
- 自反性 : 假如
R
R
R 原来是自反的 , 那么r
(
R
)
r(R)
r(R) 也是自反的 ; - 对称性 : 假如
R
R
R 原来是对称的 , 那么r
(
R
)
r(R)
r(R) 也是对称的 ; 求自反闭包 , 只是给顶点加环 , 不影响对称性 ; - 传递性 : 假如
R
R
R 原来是传递的 , 那么r
(
R
)
r(R)
r(R) 也是传递的 ; 求自反闭包 , 只是给顶点加环 , 不影响传递性 ;
仅有一个特例 : 原来
R
R
R 是传递的 , 如果求对称闭包 , 其对称闭包的传递性就不存在了 ;
表格第二列说明 ( 自反性 ) : 如果
R
R
R 关系是自反的 , 那么其 对称闭包
s
(
R
)
s(R)
s(R) 和 传递闭包
t
(
R
)
t(R)
t(R) 也是自反的 ;
R
自
反
⇒
s
(
R
)
和
t
(
R
)
自
反
R 自反 \Rightarrow s(R) 和 t(R) 自反
R自反⇒s(R)和t(R)自反
表格第三列说明 ( 对称性 ) : 如果
R
R
R 关系是对称的 , 那么其 自反闭包
r
(
R
)
r(R)
r(R) 和 传递闭包
t
(
R
)
t(R)
t(R) 也是对称的 ;
R
对
称
⇒
r
(
R
)
和
t
(
R
)
对
称
R 对称 \Rightarrow r(R) 和 t(R) 对称
R对称⇒r(R)和t(R)对称
表格第四列说明 ( 传递性 ) : 如果
R
R
R 关系是传递的 , 那么其 自反闭包
r
(
R
)
r(R)
r(R) 也是传递的 ;
R
传
递
⇒
r
(
R
)
传
递
R 传递 \Rightarrow r(R) 传递
R传递⇒r(R)传递
五、闭包复合运算
R
R
R 关系是
A
A
A 集合上的二元关系 ,
R
⊆
A
R \subseteq A
R⊆A , 且
A
A
A 集合不为空集 ,
A
≠
∅
A \not= \varnothing
A=∅
1.
r
s
(
R
)
=
s
r
(
R
)
rs(R) = sr(R)
rs(R)=sr(R) :
- rs( R ) : 先求
R
R
R 关系的 自反闭包 , 然后再求自反闭包的 对称闭包 - sr( R ) : 先求
R
R
R 关系的对称闭包 , 然后再求对称闭包的自反闭包 - 上述两个闭包运算的 结果相同
2.
r
t
(
R
)
=
t
r
(
R
)
rt(R) = tr(R)
rt(R)=tr(R)
- rt( R ) : 先求
R
R
R 关系的 自反闭包 , 然后再求自反闭包的 传递闭包 - tr( R ) : 先求
R
R
R 关系的传递闭包 , 然后再求传递闭包的自反闭包 - 上述两个闭包运算的 结果相同
3.
s
t
(
R
)
⊆
t
s
(
R
)
st(R) \subseteq ts(R)
st(R)⊆ts(R)
- st( R ) : 先求
R
R
R 关系的 对称闭包 , 然后再求对称闭包的 传递闭包 - ts( R ) : 先求
R
R
R 关系的传递闭包 , 然后再求传递闭包的对称闭包 - 上述两个闭包运算的结果 ,
t
s
(
R
)
ts(R)
ts(R) 关系 包含s
t
(
R
)
st(R)
st(R) 关系 ;
 IDEA激活码
IDEA激活码


