文章目录
- 一、关系闭包相关定理 ( 闭包运算不动点 )
- 二、关系闭包相关定理 ( 闭包运算单调性 )
- 三、关系闭包相关定理 ( 闭包运算与并运算之间的关系 )
- 四、传递闭包并集反例
一、关系闭包相关定理 ( 闭包运算不动点 )
R
R
R 关系是
A
A
A 集合上的二元关系 ,
R
⊆
A
R \subseteq A
R⊆A , 且
A
A
A 集合不为空集 ,
A
≠
∅
A \not= \varnothing
A=∅
R
R
R 关系是自反的 , 当且仅当
R
R
R 关系的自反闭包
r
(
R
)
r ( R )
r(R) 也是
R
R
R 关系本身 ;
R
自
反
⇔
r
(
R
)
=
R
R 自反 \Leftrightarrow r(R) = R
R自反⇔r(R)=R
R
R
R 关系是对称的 , 当且仅当
R
R
R 关系的对称闭包
s
(
R
)
s ( R )
s(R) 也是
R
R
R 关系本身 ;
R
对
称
⇔
s
(
R
)
=
R
R 对称 \Leftrightarrow s(R) = R
R对称⇔s(R)=R
R
R
R 关系是传递的 , 当且仅当
R
R
R 关系的传递闭包
t
(
R
)
t ( R )
t(R) 也是
R
R
R 关系本身 ;
R
传
递
⇔
t
(
R
)
=
R
R 传递 \Leftrightarrow t(R) = R
R传递⇔t(R)=R
二、关系闭包相关定理 ( 闭包运算单调性 )
R
1
,
R
2
R_1 , R_2
R1,R2 关系是
A
A
A 集合上的二元关系 ,
R
2
R_2
R2 关系包含
R
1
R_1
R1 关系 ,
R
1
⊆
R
2
⊆
A
×
A
R_1 \subseteq R_2 \subseteq A \times A
R1⊆R2⊆A×A , 且
A
A
A 集合不为空集 ,
A
≠
∅
A \not= \varnothing
A=∅
R
1
R_1
R1 关系的自反闭包 包含于
R
2
R_2
R2 关系的自反闭包
r
(
R
1
)
⊆
r
(
R
2
)
r(R_1) \subseteq r(R_2)
r(R1)⊆r(R2)
R
1
R_1
R1 关系的对称闭包 包含于
R
2
R_2
R2 关系的对称闭包
s
(
R
1
)
⊆
s
(
R
2
)
s(R_1) \subseteq s(R_2)
s(R1)⊆s(R2)
R
1
R_1
R1 关系的传递闭包 包含于
R
2
R_2
R2 关系的传递闭包
t
(
R
1
)
⊆
t
(
R
2
)
t(R_1) \subseteq t(R_2)
t(R1)⊆t(R2)
三、关系闭包相关定理 ( 闭包运算与并运算之间的关系 )
R
1
,
R
2
R_1 , R_2
R1,R2 关系是
A
A
A 集合上的二元关系 ,
R
2
R_2
R2 关系包含
R
1
R_1
R1 关系 ,
R
1
⊆
R
2
⊆
A
×
A
R_1 \subseteq R_2 \subseteq A \times A
R1⊆R2⊆A×A , 且
A
A
A 集合不为空集 ,
A
≠
∅
A \not= \varnothing
A=∅
自反闭包并集 :
R
1
R_1
R1 关系 与
R
2
R_2
R2 关系 并集 的 自反闭包 , 等于
R
1
R_1
R1 关系的自反闭包 与
R
2
R_2
R2 关系的自反闭包 的并集 ;
r
(
R
1
∪
R
2
)
=
r
(
R
1
)
∪
r
(
R
2
)
r(R_1 \cup R_2) = r(R_1) \cup r(R_2)
r(R1∪R2)=r(R1)∪r(R2)
对称闭包并集 :
R
1
R_1
R1 关系 与
R
2
R_2
R2 关系 并集 的 对称闭包 , 等于
R
1
R_1
R1 关系的对称闭包 与
R
2
R_2
R2 关系的对称闭包 的并集 ;
s
(
R
1
∪
R
2
)
=
s
(
R
1
)
∪
s
(
R
2
)
s(R_1 \cup R_2) = s(R_1) \cup s(R_2)
s(R1∪R2)=s(R1)∪s(R2)
传递闭包并集 :
R
1
R_1
R1 关系 与
R
2
R_2
R2 关系 并集 的 传递闭包 , 包含
R
1
R_1
R1 关系的传递闭包 与
R
2
R_2
R2 关系的传递闭包 的并集 ;
t
(
R
1
∪
R
2
)
⊇
t
(
R
1
)
∪
t
(
R
2
)
t(R_1 \cup R_2) \supseteq t(R_1) \cup t(R_2)
t(R1∪R2)⊇t(R1)∪t(R2)
四、传递闭包并集反例
传递闭包 的反例 :
集合
A
=
{
a
,
b
}
A = \{a, b\}
A={a,b}
关系
R
1
=
{
<
a
,
b
>
}
R_1 = \{ <a,b> \}
R1={<a,b>} , 关系
R
2
=
{
<
b
,
a
>
}
R_2 = \{ <b,a> \}
R2={<b,a>}
R
1
R_1
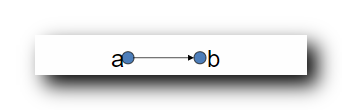
R1 关系的传递闭包 :
t
(
R
1
)
=
{
<
a
,
b
>
}
t(R_1) = \{ <a,b> \}
t(R1)={<a,b>}
R
2
R_2
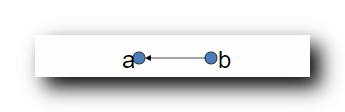
R2 关系的传递闭包 :
t
(
R
2
)
=
{
<
b
,
a
>
}
t(R_2) = \{ <b,a> \}
t(R2)={<b,a>}
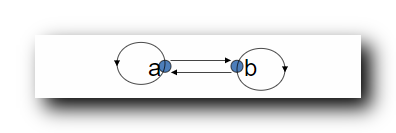
并集的闭包 :
t
(
R
1
∪
R
2
)
=
{
<
a
,
b
>
,
<
a
,
a
>
,
<
b
,
a
>
,
<
b
,
b
>
}
t(R_1 \cup R_2) = \{ <a,b> , <a,a> , <b,a> , <b,b> \}
t(R1∪R2)={<a,b>,<a,a>,<b,a>,<b,b>}
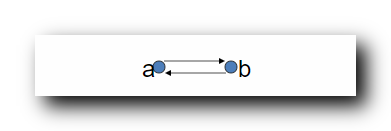
闭包的并集 :
t
(
R
1
)
∪
t
(
R
2
)
=
{
<
a
,
b
>
,
<
b
,
a
>
}
t(R_1) \cup t(R_2) = \{ <a,b> , <b, a> \}
t(R1)∪t(R2)={<a,b>,<b,a>} , 该关系是非传递的 ;
 IDEA激活码
IDEA激活码


