文章目录

一、常见的关系的性质
二、关系的性质示例
三、关系运算性质

一、常见的关系的性质

在自然数集

N

=

{

0

,

1

,

2

,

⋯

}

N=\{ 0, 1,2, \cdots \}

$N = {0, 1, 2, \dots}$ 上 , 如下关系的性质 :

1. 小于等于关系：

小于等于关系 :

符号化描述 :

≤

{

∣

∈

∧

∈

∧

≤

}

\leq = \{ <x, y> | x \in N \land y \in N \land x \leq y \}

$\leq = {< x, y > ∣ x \in N \land y \in N \land x \leq y}$

关系性质 : 自反 , 反对称 , 传递

2. 大于等于关系：

大于等于关系 :

符号化描述 :

≥

{

∣

∈

∧

∈

∧

≥

}

\geq = \{ <x, y> | x \in N \land y \in N \land x \geq y \}

$\geq = {< x, y > ∣ x \in N \land y \in N \land x \geq y}$

关系性质 : 自反 , 反对称 , 传递

3. 小于关系：

小于关系 :

符号化描述 :

{

∣

∈

∧

∈

∧

}

< = \{ <x, y> | x \in N \land y \in N \land x < y \}

$< = {< x, y > ∣ x \in N \land y \in N \land x < y}$

关系性质 : 反自反 , 反对称 , 传递

4. 大于关系：

大于关系 :

符号化描述 :

{

∣

∈

∧

∈

∧

}

> = \{ <x, y> | x \in N \land y \in N \land x > y \}

$> = {< x, y > ∣ x \in N \land y \in N \land x > y}$

关系性质 : 反自反 , 反对称 , 传递

5. 整除关系 :

整除关系 :

符号化描述 :

∣

{

∣

∈

∧

∈

∧

∣

}

| = \{ <x, y> | x \in N \land y \in N \land x | y \}

$∣ = {< x, y > ∣ x \in N \land y \in N \land x ∣ y}$

关系性质 : 反对称 , 传递

x

∣

y

x|y

$x ∣ y$ 中的

∣

|

$∣$ 符号是整除的意思 ,

x

x

$x$ 整除

y

y

$y$ ;

x

x

$x$ 整除

y

y

$y$ ,

x

x

$x$ 是除数 (分子) ,

y

y

$y$ 是被除数 (分母) ;

y

x

\dfrac{y}{x}

$\frac{y}{x}$
y

y

$y$ 能被

x

x

$x$ 整除 ,

x

x

$x$ 是除数 (分子) ,

y

y

$y$ 是被除数 (分母) ;

y

x

\dfrac{y}{x}

$\frac{y}{x}$
整除关系中 , 一定要注意 , 只能非

0

0

$0$ 整除

0

0

$0$ ,

0

0

$0$ 不能整除非

0

0

$0$ , 即

0

0

$0$ 只能作被除数 , 不能作除数 ;

6. 恒等关系 :

恒等关系 :

符号化描述 :

{

∣

∈

∧

∈

∧

}

I_N = \{ <x, y> | x \in N \land y \in N \land x = y \}

$I_{N} = {< x, y > ∣ x \in N \land y \in N \land x = y}$

关系性质 : 自反 , 对称 , 反对称 , 传递

7. 全域关系 :

全域关系 :

符号化描述 :

{

∣

∈

∧

∈

}

E_N = \{ <x, y> | x \in N \land y \in N \} = N \times N

$E_{N} = {< x, y > ∣ x \in N \land y \in N} = N \times N$

关系性质 : 自反 , 对称 , 传递

自反 , 反对称的关系 , 称为偏序关系 ;

二、关系的性质示例

关系图关系判定 :

① 自反 : 关系图中所有顶点都有环 ;
② 反自反 : 关系图中所有顶点都没有环 ;
③ 对称 : 两个顶点之间有
$2$ 个有向边 ;
④ 反对称 : 两个顶点之间有
$1$ 个有向边 ;
⑤ 传递 : 前提 $\to b , b\to c a→b,b→c 不成立默认传递 , 前提 a → b , b → c a \to b , b\to c a→b,b→c 成立必须满足 a → c a \to c a→c 存在 ;$

R

1

=

{

<

a

,

a

>

,

<

a

,

b

>

,



,

<

a

,

c

>

}

R_1 = \{ <a, a> , <a, b> , , <a,c> \}

$R_{1} = {< a, a >, < a, b >, < b, c >, < a, c >}$ :

绘制上述关系的关系图 : 反对称 , 传递
在这里插入图片描述

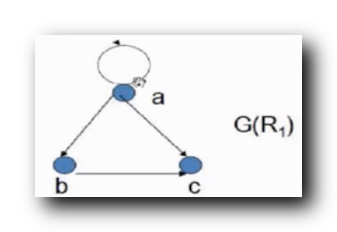
自反/反自反 : 有的顶点有环 , 有的顶点没有环 , 自反和反自反都不成立 ;

对称/反对称 : 顶点之间都是

$1$ 条有向边 , 顶点之间只有

0/1

$0 / 1$ 条边 , 是反对称的 ;

传递 :

→

a\to b, b \to c

$a \to b, b \to c$ 成立 ,

→

a \to c

$a \to c$ 存在 , 传递性成立 ;

R

2

=

{

<

a

,

a

>

,

<

a

,

b

>

,



,

<

c

,

a

>

}

R_2 = \{ <a, a> , <a, b> , , <c,a> \}

$R_{2} = {< a, a >, < a, b >, < b, c >, < c, a >}$ :

绘制上述关系的关系图 : 反对称

在这里插入图片描述

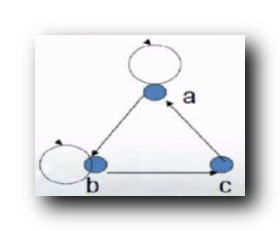
自反/反自反 : 有的顶点有环 , 有的顶点没有环 , 自反和反自反都不成立 ;

对称/反对称 : 顶点之间都是

$1$ 条有向边 , 顶点之间只有

0/1

$0 / 1$ 条边 , 是反对称的 ;

传递 :

→

a\to b, b \to c

$a \to b, b \to c$ 成立 ,

→

a \to c

$a \to c$ 不存在 , 传递性不成立 ;

R

3

=

{

<

a

,

a

>

,



,

<

a

,

b

>

,



,

<

c

,

c

>

}

R_3 = \{ <a, a> , <b, b> , <a,b> , <b,a> , <c,c> \}

$R_{3} = {< a, a >, < b, b >, < a, b >, < b, a >, < c, c >}$ :

绘制上述关系的关系图 : 自反 , 对称 , 传递

在这里插入图片描述

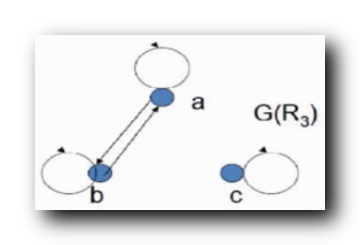
自反/反自反 : 所有顶点都有环 , 自反性成立 ;

对称/反对称 : 顶点之间都是

$0$ 或

$2$ 条有向边 , 顶点之间只有

0/2

$0 / 2$ 条边 , 是对称的 ;

传递 : 传递性成立 ;

前提 $\to b , b\to a a→b,b→a , 对应存在 a → a a \to a a→a$
前提 $\to a , a\to b b→a,a→b , 对应存在 b → b b \to b b→b$

R

4

=

{

<

a

,

a

>

,

<

a

,

b

>

,



,

<

c

,

c

>

}

R_4 = \{ <a, a> , <a,b> , <b,a> , <c,c> \}

$R_{4} = {< a, a >, < a, b >, < b, a >, < c, c >}$ :

绘制上述关系的关系图 : 对称

在这里插入图片描述

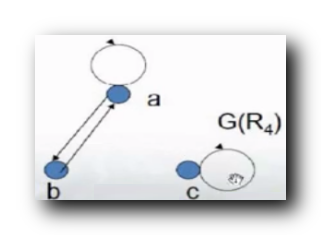
自反/反自反 : 有的顶点有环 , 有的顶点没有环 , 自反和反自反都不成立 ;

对称/反对称 : 顶点之间都是

$0$ 或

$2$ 条有向边 , 顶点之间只有

0/2

$0 / 2$ 条边 , 是对称的 ;

传递 : 传递性不成立 ;

前提 $\to b , b\to a a→b,b→a , 对应存在 a → a a \to a a→a$
前提 $\to a , a\to b b→a,a→b , 不存在对应的 b → b b \to b$
$b \to b$ , 这里传递性不成立 ;

R

5

=

{

<

a

,

a

>

,

<

a

,

b

>

,



,

<

c

,

c

>

}

R_5 = \{ <a, a> , <a,b> , <b,b> , <c,c> \}

$R_{5} = {< a, a >, < a, b >, < b, b >, < c, c >}$ :

绘制上述关系的关系图 : 自反 , 反对称 , 传递

在这里插入图片描述

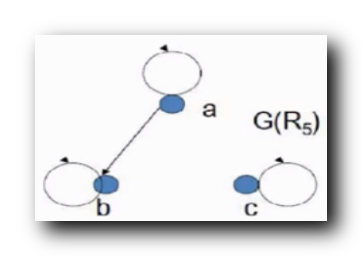
自反/反自反 : 所有顶点都有环 , 自反性成立 ;

对称/反对称 : 顶点之间都是

$0$ 或

$1$ 条有向边 , 顶点之间只有

0/1

$0 / 1$ 条边 , 是反对称的 ;

传递 : 前提不成立 , 传递性成立 ;

R

6

=

{

<

a

,

a

>

,



,



,

<

a

,

a

>

}

R_6 = \{ <a, a> , <b,a> , <b,c> , <a,a> \}

$R_{6} = {< a, a >, < b, a >, < b, c >, < a, a >}$ :

绘制上述关系的关系图 : 没有任何关系

在这里插入图片描述

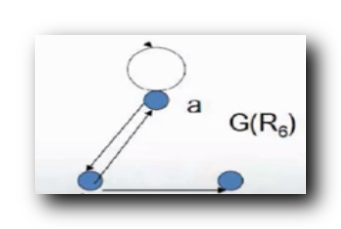
自反/反自反 : 有的顶点有环 , 有的顶点没有环 , 自反和反自反都不成立 ;

对称/反对称 : 顶点之间都是

$1$ 或

$2$ 条有向边 , 顶点之间只有

0/1

$0 / 1$ 条边是反对称 , 顶点之间只有

0/2

$0 / 2$ 条边是对称 , 上述对称/反对称都不成立 ;

传递 : 前提

→

a \to b , b \to c

$a \to b, b \to c$ , 不存在对应的

→

a \to c

$a \to c$ , 这里传递性不成立 ;

三、关系运算性质

讨论问题 : 指定性质的关系之间进行运算 , 其结果的性质 ; 如自反的两个关系进行逆序合成运算 , 结果扔是自反的 ;

下图中表格的含义是 : 如第二列 “自反” 与第三列 “

∪

R_1 \cup R_2

$R_{1} \cup R_{2}$ ” , 交叉的表格位置 , 代表关系

R_1

$R_{1}$ 与关系

R_2

$R_{2}$ 是自反的 , 其有序对交集是否是自反的 , 如果是

$1$ , 说明是自反的 , 如果没有值 , 说明不是自反的 ;

	自反	反自反	对称	反对称	传递
$R_1^{-1}, R_2^{-1} R1−1,R2−1$
$R_1 \cup R_2^{-1} R1∪R2−1$
$R_1 \cap R_2 R1∩R2$
$R_1 \circ R_2 , R_2 \circ R_1 R1∘R2,R2∘R1$
$R_1 - R_2 , R_2 - R_1 R1−R2,R2−R1$
$\sim R_1, \sim R_2 ∼R1,∼R2$

【集合论】关系性质 ( 常见的关系的性质 | 关系性质示例 | 关系运算性质 )

文章目录

一、常见的关系的性质

二、关系的性质示例

三、关系运算性质

相关推荐

一个分享Java & Python知识的社区