文章目录
- 一、传递性
- 二、传递性示例
- 三、传递性定理
一、传递性
传递性 :
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A
R
R
R 是传递的
⇔
\Leftrightarrow
⇔
∀
x
∀
y
∀
z
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
→
x
R
z
)
\forall x \forall y \forall z ( x \in A \land y \in A \land z \in A \land xRy \land yRz \to xRz )
∀x∀y∀z(x∈A∧y∈A∧z∈A∧xRy∧yRz→xRz)
⇔
\Leftrightarrow
⇔
(
∀
x
∈
A
)
(
∀
y
∈
A
)
(
∀
z
∈
A
)
[
x
R
y
∧
y
R
z
→
x
R
z
]
(\forall x \in A)(\forall y \in A)(\forall z \in A)[xRy \land yRz \to xRz]
(∀x∈A)(∀y∈A)(∀z∈A)[xRy∧yRz→xRz]
R
R
R 是非传递的
⇔
\Leftrightarrow
⇔
∃
x
∃
y
∃
z
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
→
¬
x
R
z
)
\exist x \exist y \exist z ( x \in A \land y \in A \land z \in A \land xRy \land yRz \to \lnot xRz )
∃x∃y∃z(x∈A∧y∈A∧z∈A∧xRy∧yRz→¬xRz)
传递性描述 : 任意三个元素
x
,
y
,
z
x,y,z
x,y,z ,
x
x
x 与
y
y
y 有关系
x
R
y
xRy
xRy ,
y
y
y 和
z
z
z 有关系
y
R
z
yRz
yRz ,
x
x
x 和
z
z
z 有关系
x
R
z
xRz
xRz ;
大于 , 大于等于 , 小于 , 小于等于 , 等于 , 等关系 , 是传递的 ;
二、传递性示例
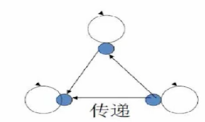
上述关系图中 , 符合 当
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz 时 , 存在
x
R
z
xRz
xRz , 则上述关系是传递的 ;
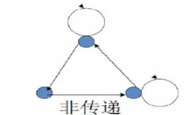
上述关系图中 , 符合 当
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz 时 , 不存在
x
R
z
xRz
xRz , 则上述关系不是传递的 ;
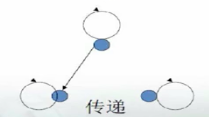
上述关系图中 , 不符合
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz 的前提条件 , 因此也不需要验证是否存在
x
R
z
xRz
xRz , 传递性默认存在 , 当出现
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz 时 , 也必须出现
x
R
z
xRz
xRz , 如果前提不成立 , 关系默认是传递的 ;
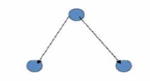
同理 , 上述关系图不符合前提 , 默认是传递的 ;
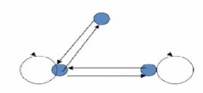
上述关系图前提条件符合 , 有
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz 时 , 不存在
x
R
z
xRz
xRz , 此时传递不成立 , 因此上述关系是非传递的 ;
三、传递性定理
传递性定理 :
R
R
R 是传递的
⇔
\Leftrightarrow
⇔
R
∘
R
⊆
R
R \circ R \subseteq R
R∘R⊆R
⇔
\Leftrightarrow
⇔
R
−
1
R^{-1}
R−1 是传递的
⇔
\Leftrightarrow
⇔
∀
i
∀
j
,
M
(
R
∘
R
)
(
i
,
j
)
≤
M
(
R
)
(
i
,
j
)
\forall i \forall j , M(R \circ R)(i,j) \leq M(R)(i,j)
∀i∀j,M(R∘R)(i,j)≤M(R)(i,j)
⇔
\Leftrightarrow
⇔
G
(
R
)
G(R)
G(R) 关系图中 ,
∀
a
i
∀
a
j
∀
a
k
\forall a_i \forall a_j \forall a_{k}
∀ai∀aj∀ak , 如果存在有向边
<
a
i
,
a
j
>
<a_i, a_j>
<ai,aj> 和
<
a
j
,
a
k
>
<a_j , a_k>
<aj,ak> , 那么必定存在有向边
<
a
j
,
a
k
>
<a_j , a_k>
<aj,ak> ;
 IDEA激活码
IDEA激活码


