文章目录
- 一、对称性
- 二、对称性示例
- 三、对称性定理
- 四、反对称性
- 五、反对称性示例
- 六、反对称性定理
- 七、对称性与反对称性示例
一、对称性
对称性 描述 :
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A
R
R
R 是对称的
⇔
\Leftrightarrow
⇔
∀
x
∀
y
(
x
∈
A
∧
y
∈
A
∧
x
R
y
→
y
R
x
)
\forall x \forall y ( x \in A \land y \in A \land xRy \to yRx )
∀x∀y(x∈A∧y∈A∧xRy→yRx)
⇔
\Leftrightarrow
⇔
(
∀
x
∈
A
)
(
∀
y
∈
A
)
[
x
R
y
→
y
R
x
]
( \forall x \in A ) (\forall y \in A)[xRy \to yRx]
(∀x∈A)(∀y∈A)[xRy→yRx]
R
R
R 是非对称的
⇔
\Leftrightarrow
⇔
∃
x
∃
y
(
x
∈
A
∧
y
∈
A
∧
x
R
y
∧
¬
y
R
x
)
\exist x \exist y ( x \in A \land y \in A \land xRy \land \lnot yRx )
∃x∃y(x∈A∧y∈A∧xRy∧¬yRx)
对称性描述 : 任选两个元素
x
,
y
x, y
x,y , 如果
x
x
x 与
y
y
y 有关系
R
R
R 即
x
R
y
xRy
xRy , 那么
y
y
y 与
x
x
x 也有关系
R
R
R 即
y
R
x
yRx
yRx ;
非对称性描述 : 只要存在一个
x
,
y
x , y
x,y 组合 ,
x
x
x 与
y
y
y 有关系
R
R
R , 但是
y
y
y 与
x
x
x 没有关系
R
R
R , 那么该关系
R
R
R 就是非对称的 ;
二、对称性示例
对称性示例 :
关系图中 , 不考虑环 , 只看两点之间的关系 , 两个顶点之间的关系都是往返箭头 , 那么就是对称的 , 有一个单向箭头 , 就不是对称的 ;
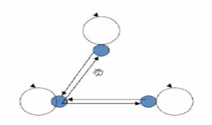
上述关系图中 , 顶点之间的箭头都是双向的 , 该关系是对称的 ;
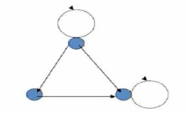
上述关系图中 , 都是单向箭头 , 有一个箭头是单向的 , 就不是对称的 ;
三、对称性定理
对称性定理 :
R
R
R 是对称的
⇔
\Leftrightarrow
⇔
R
−
1
=
R
R^{-1} = R
R−1=R
⇔
\Leftrightarrow
⇔
R
−
1
R^{-1}
R−1 是对称的
⇔
\Leftrightarrow
⇔
M
(
R
)
M(R)
M(R) 关系矩阵是对称的
⇔
\Leftrightarrow
⇔
G
(
R
)
G(R)
G(R) 的任意两个顶点之间如果有边 , 必定是两条边 ( 正向反向各一条 )
对称性 两个顶点之间 有
0
0
0 条或
2
2
2 条边 ;
四、反对称性
反对称性 :
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A
R
R
R 是反对称的
⇔
\Leftrightarrow
⇔
∀
x
∀
y
(
x
∈
A
∧
y
∈
A
∧
x
R
y
∧
y
R
x
→
x
=
y
)
\forall x \forall y ( x \in A \land y \in A \land xRy \land yRx \to x=y )
∀x∀y(x∈A∧y∈A∧xRy∧yRx→x=y)
⇔
\Leftrightarrow
⇔
(
∀
x
∈
A
)
(
∀
y
∈
A
)
[
x
R
y
∧
y
R
x
→
x
=
y
]
(\forall x \in A)(\forall y \in A)[ xRy \land yRx \to x = y ]
(∀x∈A)(∀y∈A)[xRy∧yRx→x=y]
非反对称性 :
R
R
R 是非反对称的
⇔
\Leftrightarrow
⇔
∃
x
∃
y
(
x
∈
A
∧
y
∈
A
∧
x
R
y
∧
y
R
x
∧
x
≠
y
)
\exist x \exist y ( x \in A \land y \in A \land xRy \land yRx \land x \not=y )
∃x∃y(x∈A∧y∈A∧xRy∧yRx∧x=y)
反对称就是 防止两个顶点之间有两条边 , 两个顶点之间要么有
0
0
0 条边 , 要么有
1
1
1 条边 ;
对称是 任何两个顶点之间 , 要么有
0
0
0 条边 , 要么有
2
2
2 条边 ;
如果关系图中 , 两个顶点之间没有边 , 那么该关系 既是对称的 , 又是反对称的 ; ( 环不影响对称与反对称定义 )
五、反对称性示例
反对称性 : 顶点之间没有两条边的 , 只有
0
0
0 条边 或
1
1
1 条边
对称性 : 顶点之间只有
0
0
0 条边 , 或
1
1
1 条边
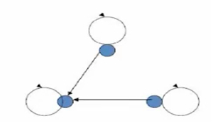
上图是反对称的 , 有两个
1
1
1 条边 , 一个
0
0
0 条边 ;
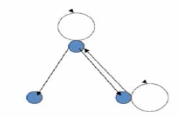
上图是非反对称的 , 有
0
0
0 条边 ,
1
1
1 条边 ,
2
2
2 条边的情况 , 是非反对称的 ;
六、反对称性定理
反对称性定理 :
R
R
R 是反对称的
⇔
\Leftrightarrow
⇔
R
−
1
∩
R
⊆
I
A
R^{-1} \cap R \subseteq I_A
R−1∩R⊆IA
⇔
\Leftrightarrow
⇔
R
−
1
R^{-1}
R−1 是反对称的
⇔
\Leftrightarrow
⇔
M
(
R
)
M(R)
M(R) 关系矩阵中 ,
∀
i
∀
j
(
i
≠
j
∧
r
i
j
=
1
→
r
j
i
=
0
)
\forall i \forall j (i \not= j \land r_{ij} = 1 \to r_{ji} = 0)
∀i∀j(i=j∧rij=1→rji=0)
⇔
\Leftrightarrow
⇔
G
(
R
)
G(R)
G(R) 关系图中 ,
∀
a
i
∀
a
j
(
i
≠
j
)
\forall a_i \forall a_j (i \not= j)
∀ai∀aj(i=j) , 如果存在有向边
<
a
i
,
a
j
>
<a_i, a_j>
<ai,aj> , 则一定不存在
<
a
j
,
a
i
>
<a_j, a_i>
<aj,ai>
R
−
1
∩
R
⊆
I
A
R^{-1} \cap R \subseteq I_A
R−1∩R⊆IA 说明 :
R
R
R 关系 与
R
−
1
R^{-1}
R−1 关系 (
R
R
R 的逆关系 ) 的交集 , 包含在 恒等关系中 ;
如果两个顶点之间有两条边 , 求逆之后 , 两个顶点的两个的两条边分别反向 , 还是相同的两条边 , 如果二者求交集 , 还是存在两条边 , 肯定不是恒等关系 , 恒等关系都是环 ; ( 不符合反对称 )
如果两个顶点之间有
1
1
1 条边 , 求逆之后 , 两个顶点之间是反向的一条边 , 两个关系的交集肯定为空 , 剩下的只有环 ; ( 反对称 )
如果两个顶点之间有
0
0
0 条边 , 求逆之后 , 两个顶点之间是
0
0
0 条边 , 两个关系的交集肯定为空 , 剩下的只有环 ; (反对称)
关系矩阵 :
M
(
R
)
M(R)
M(R) 中 ,
∀
i
∀
j
(
i
≠
j
∧
r
i
j
=
1
→
r
j
i
=
0
)
\forall i \forall j ( i \not= j \land r_{ij} = 1 \to r_{ji} = 0 )
∀i∀j(i=j∧rij=1→rji=0)
对角线以外的不能有对称的位置都是
1
1
1 的情况 , 如
r
i
j
=
1
r_{ij} = 1
rij=1 , 其对称的元素
r
j
i
r_{ji}
rji 一定不能是
1
1
1 , 必须是
0
0
0 ;
关系图 :
G
(
R
)
G(R)
G(R) 中 , 如果
∀
a
i
∀
a
j
(
i
≠
j
)
\forall a_i \forall a_j ( i \not= j )
∀ai∀aj(i=j) , 如果有有向边
<
a
i
,
a
j
>
<a_i, a_j>
<ai,aj> , 则必须没有
<
a
j
,
a
i
>
<a_j , a_i>
<aj,ai> ;
关系图中 两个顶点 只存在单向边 , 或没有边 , 不存在两个方向的边 ;
七、对称性与反对称性示例
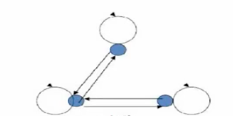
上述关系图中 , 两个顶点之间存在
0
0
0 条边 ,
2
2
2 条边 , 是对称的 ;
自反的 , 所有的顶点都有环 , 是自反的 ;
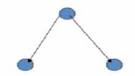
上述关系图是反对称的 , 都有 一条有向边 ;
所有的顶点 都没有环 是 反自反的 ;
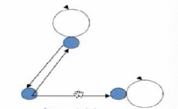
上述图中 , 有的顶点之间有
1
1
1 条边 , 有的顶点之间有
2
2
2 条边 , 既不是对称的 , 又不是反对称的 ;
有的顶点有环 , 有的顶点没有环 , 既不是 自反的 , 又不是反自反的 ;

上述关系图中 , 顶点之间都是
0
0
0 条边 ;
顶点之间是
0
0
0 条边 /
2
2
2 条边 是对称的 ;
顶点之间是
0
0
0 条边 /
1
1
1 条边 是反对称的 ;
上述关系图 既是 对称的 , 又是反对称的 ;
有的顶点有环 , 有的顶点没有环 , 既不是 自反的 , 又不是反自反的 ;
 IDEA激活码
IDEA激活码


