文章目录
- 一、关系矩阵
- 二、关系矩阵示例
- 三、关系矩阵性质
- 四、关系矩阵运算
- 五、关系图
- 六、关系图示例
- 七、关系表示相关性质
一、关系矩阵
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
,
R
⊆
A
×
A
A = \{ a_1, a_2 , \cdots , a_n \} , R \subseteq A \times A
A={a1,a2,⋯,an},R⊆A×A
R
R
R 使用 关系矩阵 表示 :
M
(
R
)
=
(
r
i
j
)
n
×
n
M(R) = (r_{ij})_{n\times n}
M(R)=(rij)n×n
关系矩阵取值 :
M
(
R
)
(
i
,
j
)
=
r
i
j
=
{
1
,
a
i
R
a
j
0
,
无
关
系
M(R)(i, j) = r_{ij} =\begin{cases} 1, & a_i R a_j \\ 0, & 无关系 \end{cases}
M(R)(i,j)=rij={1,0,aiRaj无关系
关系矩阵定义说明 :
A
A
A 是个
n
n
n 元集 ( 集合中有
n
n
n 个元素 ) ,
R
R
R 是
A
A
A 上的二元关系 ,
R
R
R 的关系矩阵是
n
×
n
n \times n
n×n 的方阵 , 第
i
i
i 行第
j
j
j 列位置的元素
r
i
j
r_{ij}
rij 取值只能是
0
0
0 或
1
1
1 ;
关系矩阵取值说明 :
如果
r
i
j
=
1
r_{ij} = 1
rij=1 , 则说明
A
A
A 集合中 第
i
i
i 个元素与第
j
j
j 个元素具有关系
R
R
R , 记作 :
a
i
R
a
j
a_i R a_j
aiRaj ;
如果
r
i
j
=
0
r_{ij} = 0
rij=0 , 则说明
A
A
A 集合中 第
i
i
i 个元素与第
j
j
j 个元素没有关系
R
R
R ;
关系矩阵本质 : 关系矩阵中 , 每一行对应着
A
A
A 集合中的元素 , 每一列也对应着
A
A
A 集合中的元素 , 行列交叉的位置的值 (
0
0
0 或
1
1
1 ) 表示
A
A
A 集合中第
i
i
i 个元素与第
j
j
j 个元素构成的有序对是否有关系
R
R
R ;
二、关系矩阵示例
A
=
{
a
,
b
,
c
}
A = \{ a, b, c \}
A={a,b,c}
R
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
}
R_1 = \{ <a, a>, <a,b> , <b,a> , <b,c> \}
R1={<a,a>,<a,b>,<b,a>,<b,c>}
R
2
=
{
<
a
,
b
>
,
<
a
,
c
>
,
<
b
,
c
>
}
R_2 = \{ <a,b> , <a,c> , <b,c> \}
R2={<a,b>,<a,c>,<b,c>}
使用关系矩阵表示上述
R
1
,
R
2
R_1 , R_2
R1,R2 两个关系 :
R
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
}
R_1 = \{ <a, a>, <a,b> , <b,a> , <b,c> \}
R1={<a,a>,<a,b>,<b,a>,<b,c>} 其中 :
-
<
a
,
a
>
<a, a>
<a,a> :a
a
a 是第1
1
1 个元素 ,a
a
a 是第1
1
1 个元素 , 第1
1
1 行第1
1
1 列元素是1
1
1 -
<
a
,
b
>
<a, b>
<a,b> :a
a
a 是第1
1
1 个元素 ,b
b
b 是第2
2
2 个元素 , 第1
1
1 行第2
2
2 列元素是1
1
1 -
<
b
,
a
>
<b, a>
<b,a> :b
b
b 是第2
2
2 个元素 ,a
a
a 是第1
1
1 个元素 , 第2
2
2 行第1
1
1 列元素是1
1
1 -
<
b
,
c
>
<b, c>
<b,c> :b
b
b 是第2
2
2 个元素 ,c
c
c 是第3
3
3 个元素 , 第2
2
2 行第3
3
3 列元素是1
1
1 - 其余全是
0
0
0
M
(
R
1
)
=
[
1
1
0
1
0
1
0
0
0
]
M(R_1) = \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R1)=⎣⎢⎢⎢⎢⎡110100010⎦⎥⎥⎥⎥⎤
R
2
=
{
<
a
,
b
>
,
<
a
,
c
>
,
<
b
,
c
>
}
R_2 = \{ <a,b> , <a,c> , <b,c> \}
R2={<a,b>,<a,c>,<b,c>} 其中 :
-
<
a
,
b
>
<a, b>
<a,b> :a
a
a 是第1
1
1 个元素 ,b
b
b 是第2
2
2 个元素 , 第1
1
1 行第2
2
2 列元素是1
1
1 -
<
a
,
c
>
<a, c>
<a,c> :a
a
a 是第1
1
1 个元素 ,c
c
c 是第3
3
3 个元素 , 第1
1
1 行第3
3
3 列元素是1
1
1 -
<
b
,
c
>
<b, c>
<b,c> :b
b
b 是第2
2
2 个元素 ,c
c
c 是第3
3
3 个元素 , 第2
2
2 行第3
3
3 列元素是1
1
1 - 其余全是
0
0
0
M
(
R
2
)
=
[
0
1
1
0
0
1
0
0
0
]
M(R_2) = \begin{bmatrix} 0 & 1 & 1 \\\\ 0 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R2)=⎣⎢⎢⎢⎢⎡000100110⎦⎥⎥⎥⎥⎤
三、关系矩阵性质
有序对集合表达式 与 关系矩阵 可以唯一相互确定
性质一 : 逆运算相关性质
M
(
R
−
1
)
=
(
M
(
R
)
)
T
M(R^{-1}) = (M(R))^T
M(R−1)=(M(R))T
M
(
R
−
1
)
M(R^{-1})
M(R−1) 关系的逆 的 关系矩阵
与
(
M
(
R
)
)
T
(M(R))^T
(M(R))T 关系矩阵 的 逆
这两个矩阵是相等的 ;
性质二 : 合成运算相关性质
M
(
R
1
∘
R
2
)
=
M
(
R
2
)
∙
M
(
R
1
)
M(R_1 \circ R_2) = M(R_2) \bullet M(R_1)
M(R1∘R2)=M(R2)∙M(R1)
∙
\bullet
∙ 是矩阵的 逻辑乘法 , 计算 矩阵
r
i
j
r_{ij}
rij 的值 第
i
i
i 行 乘以 第
j
j
j 列 , 逐位 逻辑相乘 , 再将逻辑相乘结果再 逻辑相加 ;
上述 逻辑乘法使用
∧
\land
∧ 运算 , 逻辑加法使用
∨
\lor
∨ 运算 ;
四、关系矩阵运算
A
=
{
a
,
b
,
c
}
A = \{ a, b, c \}
A={a,b,c}
R
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
}
R_1 = \{ <a, a>, <a,b> , <b,a> , <b,c> \}
R1={<a,a>,<a,b>,<b,a>,<b,c>}
R
2
=
{
<
a
,
b
>
,
<
a
,
c
>
,
<
b
,
c
>
}
R_2 = \{ <a,b> , <a,c> , <b,c> \}
R2={<a,b>,<a,c>,<b,c>}
在上面的示例中 , 已经求出两个关系矩阵 ;
M
(
R
1
)
=
[
1
1
0
1
0
1
0
0
0
]
M(R_1) = \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R1)=⎣⎢⎢⎢⎢⎡110100010⎦⎥⎥⎥⎥⎤ ,
M
(
R
2
)
=
[
0
1
1
0
0
1
0
0
0
]
M(R_2) = \begin{bmatrix} 0 & 1 & 1 \\\\ 0 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R2)=⎣⎢⎢⎢⎢⎡000100110⎦⎥⎥⎥⎥⎤
1. 求
M
(
R
−
1
)
,
M
(
R
2
−
1
)
M(R^{-1}) , M(R_2^{-1})
M(R−1),M(R2−1)
直接将矩阵转置 , 即可获取 关系的逆的关系矩阵 ;
M
(
R
1
−
1
)
=
(
M
(
R
1
)
)
T
=
[
1
1
0
1
0
0
0
1
0
]
M(R_1^{-1}) = (M(R_1))^T = \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 0 \\\\ 0 & 1 & 0 \end{bmatrix}
M(R1−1)=(M(R1))T=⎣⎢⎢⎢⎢⎡110101000⎦⎥⎥⎥⎥⎤
M
(
R
2
−
1
)
=
(
M
(
R
2
)
)
T
=
[
0
0
0
1
0
0
1
1
0
]
M(R_2^{-1}) = (M(R_2))^T = \begin{bmatrix} 0 & 0 & 0 \\\\ 1 & 0 & 0 \\\\ 1 & 1 & 0 \end{bmatrix}
M(R2−1)=(M(R2))T=⎣⎢⎢⎢⎢⎡011001000⎦⎥⎥⎥⎥⎤
R
1
−
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
c
,
b
>
}
R_1^{-1} = \{ <a, a> , <a, b> , <b,a> , <c,b> \}
R1−1={<a,a>,<a,b>,<b,a>,<c,b>}
R
2
−
1
=
{
<
b
,
a
>
,
<
c
,
a
>
,
<
c
,
b
>
}
R_2^{-1} = \{ <b, a> , <c,a> , <c,b> \}
R2−1={<b,a>,<c,a>,<c,b>}
2. 求
M
(
R
1
∘
R
1
)
M( R_1 \circ R_1 )
M(R1∘R1)
M
(
R
1
∘
R
1
)
=
M
(
R
1
)
∙
M
(
R
1
)
M( R_1 \circ R_1 ) = M(R_1) \bullet M(R_1)
M(R1∘R1)=M(R1)∙M(R1)
其中的
∙
\bullet
∙ 是两个矩阵的逻辑乘法 , 加法使用
∨
\lor
∨ , 乘法使用
∧
\land
∧
M
(
R
1
)
∙
M
(
R
1
)
=
[
1
1
0
1
0
1
0
0
0
]
∙
[
1
1
0
1
0
1
0
0
0
]
=
[
1
1
1
1
1
0
0
0
0
]
M(R_1) \bullet M(R_1) = \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\\\ 1 & 1 & 0 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R1)∙M(R1)=⎣⎢⎢⎢⎢⎡110100010⎦⎥⎥⎥⎥⎤∙⎣⎢⎢⎢⎢⎡110100010⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡110110100⎦⎥⎥⎥⎥⎤
矩阵的逻辑乘法 : 结果矩阵的第
i
i
i 行 , 第
j
j
j 列元素的值为 , 第
i
i
i 行的三个元素 分别与上第
j
j
j 列的三个元素 , 然后三个结果进行或运算 , 最终结果就是 矩阵的第
i
i
i 行 , 第
j
j
j 列元素的值 ;
R
1
∘
R
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
a
,
c
>
,
<
b
,
a
>
,
<
b
,
b
>
}
R_1 \circ R_1 = \{ <a,a> , <a,b> , <a,c> , <b,a>, <b,b> \}
R1∘R1={<a,a>,<a,b>,<a,c>,<b,a>,<b,b>}
3. 求
M
(
R
1
∘
R
2
)
M( R_1 \circ R_2 )
M(R1∘R2)
M
(
R
1
∘
R
2
)
=
M
(
R
2
)
∙
M
(
R
1
)
M( R_1 \circ R_2 ) = M(R_2) \bullet M(R_1)
M(R1∘R2)=M(R2)∙M(R1)
其中的
∙
\bullet
∙ 是两个矩阵的逻辑乘法 , 加法使用
∨
\lor
∨ , 乘法使用
∧
\land
∧
特别注意 , 合成的顺序是逆序合成 , 后者关系矩阵在前 , 前者关系矩阵在后
M
(
R
1
)
∙
M
(
R
2
)
=
[
0
1
1
0
0
1
0
0
0
]
∙
[
1
1
0
1
0
1
0
0
0
]
=
[
1
0
1
0
0
0
0
0
0
]
M(R_1) \bullet M(R_2) =\begin{bmatrix} 0 & 1 & 1 \\\\ 0 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 1 & 0 \\\\ 1 & 0 & 1 \\\\ 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \end{bmatrix}
M(R1)∙M(R2)=⎣⎢⎢⎢⎢⎡000100110⎦⎥⎥⎥⎥⎤∙⎣⎢⎢⎢⎢⎡110100010⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡100000100⎦⎥⎥⎥⎥⎤
矩阵的逻辑乘法 : 结果矩阵的第
i
i
i 行 , 第
j
j
j 列元素的值为 , 第
i
i
i 行的三个元素 分别与上第
j
j
j 列的三个元素 , 然后三个结果进行或运算 , 最终结果就是 矩阵的第
i
i
i 行 , 第
j
j
j 列元素的值 ;
R
1
∘
R
2
=
{
<
a
,
a
>
,
<
a
,
c
>
}
R_1 \circ R_2 = \{ <a,a>, <a,c> \}
R1∘R2={<a,a>,<a,c>}
五、关系图
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
,
R
⊆
A
×
A
A = \{ a_1, a_2 , \cdots , a_n \} , R \subseteq A \times A
A={a1,a2,⋯,an},R⊆A×A
R
R
R 的关系图 :
- 顶点 :
∘
\circ
∘ 表示A
A
A 集合中的元素 ; - 有向边 :
→
\rightarrow
→ 表示R
R
R 中的元素 ; -
a
i
R
a
j
a_i R a_j
aiRaj 就是从顶点a
i
a_i
ai 到 顶点a
j
a_j
aj 的有向边<
a
i
,
a
j
>
<a_i , a_j>
<ai,aj> ;
六、关系图示例
A
=
{
a
,
b
,
c
}
A = \{ a, b, c \}
A={a,b,c}
R
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
b
,
c
>
}
R_1 = \{ <a, a> , <a,b> , <b,a> , <b,c> \}
R1={<a,a>,<a,b>,<b,a>,<b,c>} 关系图表示方式 :
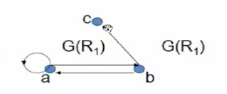
R
2
=
{
<
a
,
b
>
,
<
a
,
c
>
,
<
b
,
c
>
}
R_2 = \{ <a,b>, <a,c>, <b,c> \}
R2={<a,b>,<a,c>,<b,c>} 使用关系图表示 :
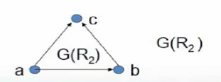
R
1
−
1
=
{
<
a
,
a
>
,
<
a
,
b
>
,
<
b
,
a
>
,
<
c
,
b
>
}
R_1^{-1} = \{ <a,a>, <a,b>, <b,a> , <c,b> \}
R1−1={<a,a>,<a,b>,<b,a>,<c,b>}
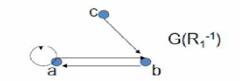
R
2
−
1
=
{
<
b
,
a
>
,
<
c
,
a
>
,
<
c
,
b
>
}
R_2^{-1} = \{ <b,a> , <c,a> , <c,b> \}
R2−1={<b,a>,<c,a>,<c,b>}
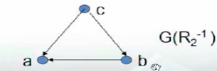
七、关系表示相关性质
A
A
A 集合中的元素 , 标定次序后 , 即生成了
A
A
A 上的关系 ,
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A , 有如下性质 :
- 关系图
G
(
R
)
G(R)
G(R) 与 关系的R
R
R 的集合表达式 ( 有序对集合 ) , 可以 唯一确定 ; - 关系
R
R
R 的集合表达式 , 关系矩阵M
(
R
)
M(R)
M(R) , 关系图G
(
R
)
G(R)
G(R) , 都是一一对应的 ;
R
⊆
A
×
B
R \subseteq A \times B
R⊆A×B
- 集合
A
A
A 中有n
n
n 个元素 ,∣
A
∣
=
n
|A| = n
∣A∣=n - 集合
B
B
B 中有m
m
m 个元素 ,∣
B
∣
=
m
|B| = m
∣B∣=m - 关系矩阵
M
(
R
)
M(R)
M(R) 是n
×
m
n \times m
n×m 阶矩阵 ; - 关系图
G
(
R
)
G(R)
G(R) 有向边都是从A
A
A 集合中的元素 指向B
B
B 集合中的元素
 IDEA激活码
IDEA激活码


