【集合论】偏序关系相关题目解析 ( 偏序关系中的特殊元素 | 绘制哈斯图 | 链

文章目录

- - - 偏序关系中的特殊元素问题
    - 偏序关系证明哈斯图链反链

偏序关系中的特殊元素问题

题目 : 偏序关系特殊元素 ;

条件 : 下图是某一偏序集 $\preceq> <A,⪯> 的哈斯图 , 其中 A = { a , b , ⋯   , k } A=\{a,b,\cdots,k\}$
$A = {a, b, \dots, k}$
问题
$1$ :

B

1

=

{

a

,

c

,

d

,

e

}

B_1 = \{a,c,d,e\}

$B_{1} = {a, c, d, e}$ 是什么链 ;
问题
$2$ :

B

2

=

{

a

,

e

,

h

}

B_2 = \{a,e,h\}

$B_{2} = {a, e, h}$ 是什么链 ;
问题
$3$ :

B

3

=

{

b

,

g

}

B_3 = \{b,g\}

$B_{3} = {b, g}$ 是什么链 ;
问题
$4$ :

B

4

=

{

g

,

h

,

k

}

B_4 = \{g,h,k\}

$B_{4} = {g, h, k}$ 是什么链 ;
问题
$5$ :

B

5

=

{

a

}

B_5 = \{a\}

$B_{5} = {a}$ 是什么链 ;
问题
$6$ :

B

6

=

{

a

,

b

,

g

,

h

}

B_6 = \{a, b, g, h\}

$B_{6} = {a, b, g, h}$ 是什么链 ;
问题
$7$ :

B

1

B_1

$B_{1}$ 的上界, 下界, 上确界 , 下确界 ;
问题
$8$ :

B

4

B_4

$B_{4}$ 的上界, 下界, 上确界 , 下确界 ;

在这里插入图片描述

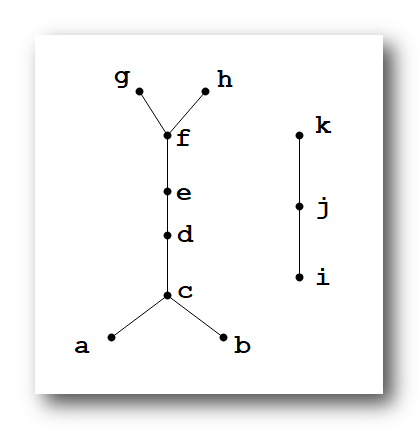
解答 :

① 问题

1

1

$1$ :

B

1

=

{

a

,

c

,

d

,

e

}

B_1 = \{a,c,d,e\}

$B_{1} = {a, c, d, e}$ 是一条长为 4 的链 ;
这四个元素互相之间是可比的 ; 并且也是覆盖的 ,

e

e

$e$ 覆盖

d

d

$d$ ,

d

d

$d$ 覆盖

c

c

$c$ ,

c

c

$c$ 覆盖

a

a

$a$ ;

② 问题

2

2

$2$ :

B

2

=

{

a

,

e

,

h

}

B_2 = \{a,e,h\}

$B_{2} = {a, e, h}$ 是一条长为 3 的链 ;

a

,

e

,

h

a,e,h

$a, e, h$ 之间都是可比的 , 但没有覆盖关系 , 即他们之间都有其它元素相隔 , 这也是链 ;
集合中有

n

n

$n$ 个元素 , 且这些元素可比 , 那么这个集合就是一个长为

n

n

$n$ 的链 , 中间可以隔着其它元素 ;

③ 问题

3

3

$3$ :

B

3

=

{

b

,

g

}

B_3 = \{b,g\}

$B_{3} = {b, g}$ 是一条长为 2 的链 ;

b

,

g

b,g

$b, g$ 之间隔着 4 个元素 , 但这个集合中元素是可比的 , 也是链, 长度为集合的元素个数 ;

④ 问题

4

4

$4$ :

B

4

=

{

g

,

h

,

k

}

B_4 = \{g,h,k\}

$B_{4} = {g, h, k}$ 是一条长为 3 的反链 ;
集合中的元素 , 都不可比 , 那这个集合就是反链 ;
如果一部分可比 , 另一部分不可比 , 那这个集合什么都不是 , 既不是链 , 也不是反链 ;

⑤ 问题

5

5

$5$ :

B

5

=

{

a

}

B_5 = \{a\}

$B_{5} = {a}$ 是一条长为 1 的链 , 同时也是一条长为 1 的反链 ;
如果集合中只有一个元素 , 那么该集合既是链 , 又是反链 , 长度为

1

1

$1$ ;

⑥ 问题

6

6

$6$ :

B

6

=

{

a

,

b

,

g

,

h

}

B_6 = \{a, b, g, h\}

$B_{6} = {a, b, g, h}$ 既不是链 , 也不是反链 ;

g

,

a

g,a

$g, a$ 是可比的,

h

,

a

h,a

$h, a$ 是可比的 ,

g

,

b

g,b

$g, b$ 是可比的 ,

h

,

b

h,b

$h, b$ 是可比的 ,

g

,

h

g,h

$g, h$ 不可比 ,

a

,

b

a,b

$a, b$ 不可比 , 因此其既不是链 , 也不是反链 ;

⑦ 问题

7

7

$7$ :

上界问题 :

1> 上界集合 : $B_1 = \{a,c,d,e\} B1={a,c,d,e} 上界集合为 { e , f , g , h } \{e, f,g,h\}$
${e, f, g, h}$ ;
2> 上确界 ( 最小上界 ) : $B_1 B1 的上确界是 e e$
$e$ , 即上界集合的最小元 ;

注意 :
上界是一个元素 , 一个集合的上界可能有很多个, 上界集合是上界元素的集合 ;
上界集合中的最小元是上确界或最小上界 ;
集合不一定有上界 ( 有可能上面有两个极大元, 互不可比 ) , 有上界不一定有上确界 ;

下界问题 :

1> 下界集合 : $B_1 = \{a,c,d,e\} B1={a,c,d,e} 下界集合为 { a } \{a\}$
${a}$ ;
2> 下确界 ( 最大下界 ) : $B_1 B1 的下确界是 a a$
$a$ , 即下界集合的最大元 ;

注意 :
下界是一个元素 , 一个集合的下界可能有很多个, 下界集合是下界元素的集合 ;
下界集合中的最大元是下确界或最大下界 ;
集合不一定有下界 ( 有可能下面有两个极小元, 互不可比 ) , 有下界不一定有下确界 ( 最大下界 ) ;

求一个集合的下界和上界 , 注意从集合的最小元 ( 下界 ) 和最大元 ( 上界 ) 开始算 , 不要忽略这两个元素 ;

⑧ 问题

8

8

$8$ :

B

4

=

{

g

,

h

,

k

}

B_4 = \{g,h,k\}

$B_{4} = {g, h, k}$ 是反链 , 其没有上界和下界 , 自然也不存在上确界和下确界 ;
反链是没有上界和下界的 , 元素之间都不可比 ;

偏序关系证明哈斯图链反链

题目 :

条件 : 集合
$A$ 上的整除关系 ;
问题 1 : 证明该关系是偏序关系 ;
问题 2 : 画出关系的哈斯图
问题 3 : 确定
$A$ 中的最长链 ; 写出所有最长链 ;
问题4 :
$A$ 中的元素至少可以划分成多少个互不相交的反链 , 并写出这些反链 ;

解答 :

问题 1 : 偏序关系证明 :

① 写出

120

120

$120$ 的因子集合 : 先列出其素因子 , 然后使用素因子组合即可 ;
( 注意

x

x

$x$ 整除

y

y

$y$ ,

x

x

$x$ 是较小的数 , 是除数 ,

y

y

$y$ 是较大的数 , 是被除数 ,

除

数

∣

被

除

数

除数 | 被除数

$除数 ∣ 被除数$ 是整除关系的表示 )

{

120

}

A=\{1, 2,3,4,5,6,8,10,12,15,20,24,30, 40,60,120\}

$A = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}$

② 证明偏序关系需要证明其三个性质自反反对称传递 ;

1.证明自反性 : $\forall x \in A ∀x∈A , x x x 本身肯定能整除它自己 , x x x 与 x x x 是可比的 , 因此 x x$
$x$ 是自反的 ;
2.证明反对称性 :
$1$ ;
3.证明传递性 :
$4$ ;

问题 2 : 画哈斯图 : 先画出

1

1

$1$ , 从底下向上画, 画完后逐个检查是否有遗漏 ;

在这里插入图片描述

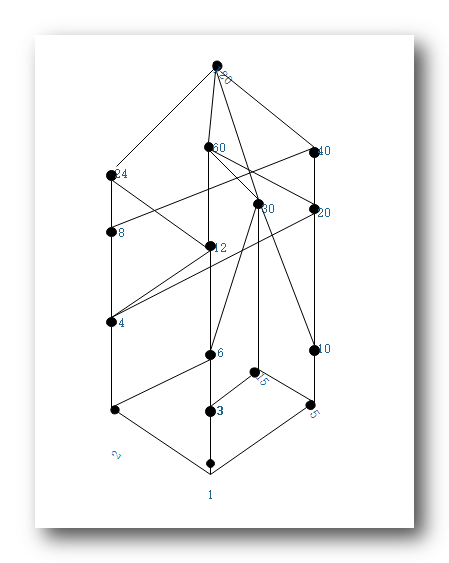
问题 3 : 确定最长链并找出最长链 :

① 逐个寻找 , 最长链为 6 , 从底部到上面从左到右逐个分支进行遍历写出长度为 6 的链 ;
从底部

1

1

$1$ 开始写 , 最左侧的链为 :

{

120

}

\{1,2,4,8,24,120\}

${1, 2, 4, 8, 24, 120}$

这个最左侧链从顶部向下走 , 从

8

8

$8$ 开始有个分支 , 写下这个链

{

120

}

\{1,2,4,8,40,120\}

${1, 2, 4, 8, 40, 120}$

继续往下走 ,

4

4

$4$ 的位置有个分支 , 其下对应着

3

3

$3$ 个分支分别是 :

{

120

}

\{1,2,4,12,24,120\}

${1, 2, 4, 12, 24, 120}$

{

120

}

\{1,2,4,12,60,120\}

${1, 2, 4, 12, 60, 120}$

{

120

}

\{1,2,4,20,60,120\}

${1, 2, 4, 20, 60, 120}$

继续往下走 ,

2

2

$2$ 的位置有分支 , 对应

给出参考答案 , 不在详细列出 :

1→2→4→8→24→120

1→2→4→8→40→120

1→2→4→12→24→120

1→2→4→12→60→120

1→2→6→12→60→120

1→2→6→30→60→120

1→3→6→12→24→120

1→3→6→12→60→120

1→3→6→30→60→120

1→3→15→30→60→120

1→5→10→20→40→120

1→5→10→30→60→120

1→5→15→30→60→120

问题 4 : 集合

A

A

$A$ 至少划分成多少互不相交的反链 , 完整写出这些反链 :

分析 : 将集合

A

A

$A$ 划分成最多的反链个数是

16

16

$16$ 个 , 即每个元素都划分成一个单独的反链 ;

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

}

{

120

}

\{\{1\}, \{2\}, \{3\}, \{4\}, \{5\}, \{6\}, \{8\}, \{10\}, \{12\}, \{15\}, \{20\}, \{24\}, \{30\}, \{ 40\}, \{60\}, \{120\}\}

${{1}, {2}, {3}, {4}, {5}, {6}, {8}, {10}, {12}, {15}, {20}, {24}, {30}, {40}, {60}, {120}}$

现在需要将其尽可能多的将上述集合进行合并 , 每个集合必须是反链 :

{

}

{

120

}

{

}

{

}

{

}

{

}

\{ \{ 1 \}, \{ 120 \}, \{2,3,5\} , \{ 4,6,15,10 \} , \{ 8, 12 , 30, 20 \} , , \{ 24, 60 , 40 \} \}

${{1}, {120}, {2, 3, 5}, {4, 6, 15, 10}, {8, 12, 30, 20},, {24, 60, 40}}$

结果 : 至少能划分成 6 个互不相交的反链 ;

技巧 : 哈斯图横向没有关联的一条线可以组成一条反链 ;

【集合论】偏序关系相关题目解析 ( 偏序关系中的特殊元素 | 绘制哈斯图 | 链 | 反链 )

文章目录

偏序关系中的特殊元素问题

偏序关系证明哈斯图链反链

相关推荐

一个分享Java & Python知识的社区

文章目录

偏序关系中的特殊元素问题

偏序关系证明 哈斯图 链 反链

相关推荐

一个分享Java & Python知识的社区

偏序关系证明哈斯图链反链