之前写过一篇文章《如何计算IP或ICMP协议首部里的checksum字段》,采用的方法是:感兴趣的可以点击下面的链接,所采用的方法是:反码求和法,核心思想是先求和,再取反,今天学习一种更复杂的算法CRC-8、CRC-16或CRC-32算法
我们知道,反码求和法用的是加法
而CRC算法,用的是“除法”,这里的“除法”指的不是我们平时生活中所说的十进制除法,而是二进制中的异或取余
我们以CRC8的算法为例
既然是“除法”,肯定要有除数和被除数
被除数指的是需要被CRC校验的数据,除数根据CRC算法的不同,除数也不同,在CRC校验中,把除数称之为生成多项式
比如
CRC-8的多项式公式为:x8 + x2 + x + 1,
表示:1 0000 0111
值为0x107
CRC-8/MAXIM的多项式公式为:x8 + x5 + x4 + 1
表示:1 0011 0001
值为0x131
CRC-16/CCITT的多项式公式为:x16 + x12 + x5 + 1
表示:1 00010000 00100001
值为0x11021
可以看出
- x8表示bit8为1,x5表示bit5为1,1表示bit0为1,其他位则为0
- CRC-8的多项式共9个bit,CRC-16的多项式共17个bit,多项式总比CRC校验值多一个bit位
- 多项式的最高位和最低位总是为1
我们先看一下具体的算法,然后再分析为什么要这样设计
假设有一个数0x97,我想用CRC-8计算它的校验和,生成多项式为x8 + x2 + x + 1
计算方式是这样的

CRC-8是计算数据的校验和,这个校验和是8个bit,所以需要在数据后填补值为0的8个bit位
然后用多项式去除以它,也就是做异或操作,得到的值如果高位为0,则去掉,并把低位的0补齐,然后继续和多项式做异或操作,直到所有bit位全部补完,判断最后的余数是否是否还能被9个bit的多项式异或,如果不能,就说明是最终的余数,也就是计算得到的校验和
这里要注意,如果最终的余数不满8个bit,需要在高位补0
为什么不用得到的商呢,因为商表示的是异或的次数,并不具有唯一性,无法用来验证数据的完整性
从上面的计算中也能看出,这种运算方式是通过多次异或运算,来达到消除高位的1和0,直到剩下最终的余数,所以多项式的最高位必须为1
而为什么多项式的bit位的个数要比校验和的位数多1,这是为了遇1移位(我理解的)
为什么这样说呢,我们可以通过计算机中不同的计算方式来对比
上面说的计算方法是CRC的算法核心,但是在计算机系统中,算法是这个算法,只是计算方式会有一些不同
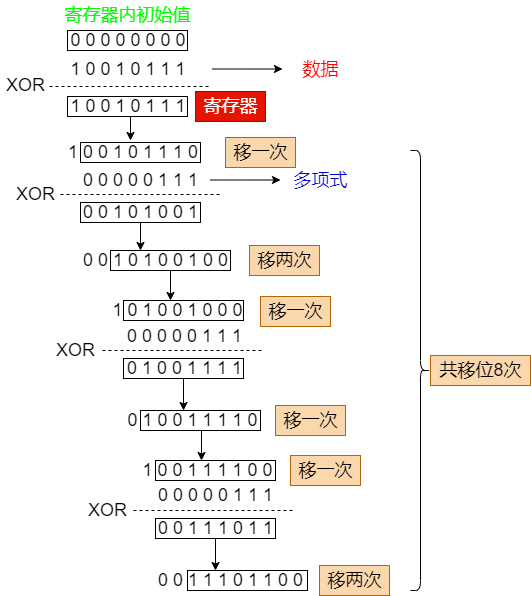
在系统中,首先会定义一个寄存器,用来存放校验值,如果是CRC-8,就存放一个8位bit值,初始值要么是0xFF,要么是0x00(要么是高电平,要么是低电平)
这时候来了一个数0x97,首先和这个初始值做异或运算,得到的新值存放寄存器
按照上面的例子,是0x97和多项式做运算,所以能看出,寄存器中的初始值应该为0x00,因为0x97和0x00做异或,得到的还是0x97,如果上面是0x97和0xFF做异或得到的值,与多项式做运算,那么初始值就应该是0xFF
所以上面的例子中,用来与多项式做除法的数,应该是和寄存器初始值做了异或运算后的值,上面没有提到这个,需要注意
0x97与初始值0x00做完异或后,得到的值,需要判断高位是否为0,如果为0,则把高位的0移出寄存器,低位补0,直到高位为1
如果高位为1,则把1移出,低位补0后,用多项式和寄存器里的值进行异或运算
直到移位8次,得到的值就是校验和
注意这种计算方式的多项式就没有bit8这一位了
我们看一下这种方式是如何计算的
可以看出,最终的校验和也是一样的
用寄存器这种方式,遇0直接移位,遇1移位后与多项式(bit7-bit0)异或,而第一张图里描绘的,只有遇0才移位,遇1会让其和多项式(bit8-bit0)异或,这时候高位的1和bit8异或,肯定为0,0最终还是会被去掉,而其他几位和bit7-bit0异或,不正是寄存器遇1移位后和bit7-bit0异或嘛
所以你现在知道bit8一定要为1的原因了吗
那么为什么要移位8次呢,我觉得应该是计算机里的最小存储单元为1个字节,8个bit,移位8次,这8个bit位全部移出,而异或得到的数,是一个全新的数
那么CRC-16呢,也是数据里的每个字节移位8次,异或运算最终得到的数,只是寄存器的大小是16位,多项式是16位,因为数据还是以每8个bit为单元的字节数
我们来对比下这两张图
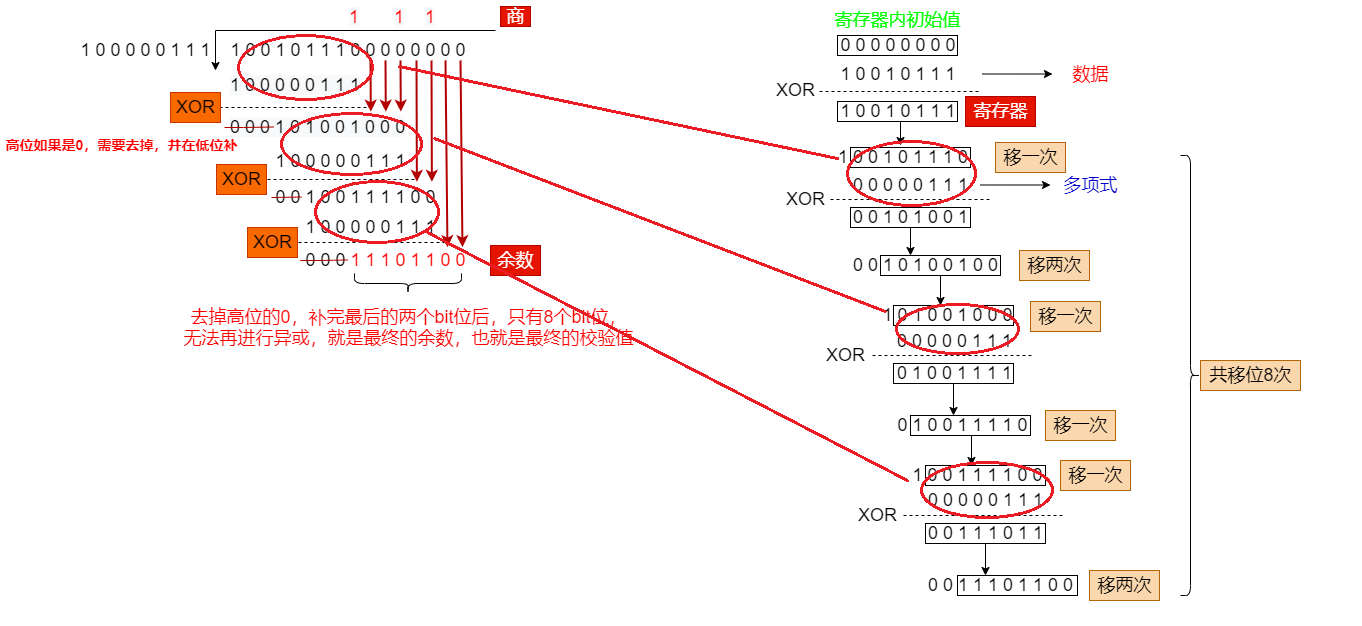
可以看出,他们的算法相同,只是计算方式不同
如果是人工来算,当然不可能是手算了,肯定需要编写脚本,要么是按照上面的计算方式编写,但是这种方式计算量太大
或者也可以拿到CRC校验对应的crc表格,它把每个值的crc校验和计算出来,放在了一张表格中,省去了大量的计算过程
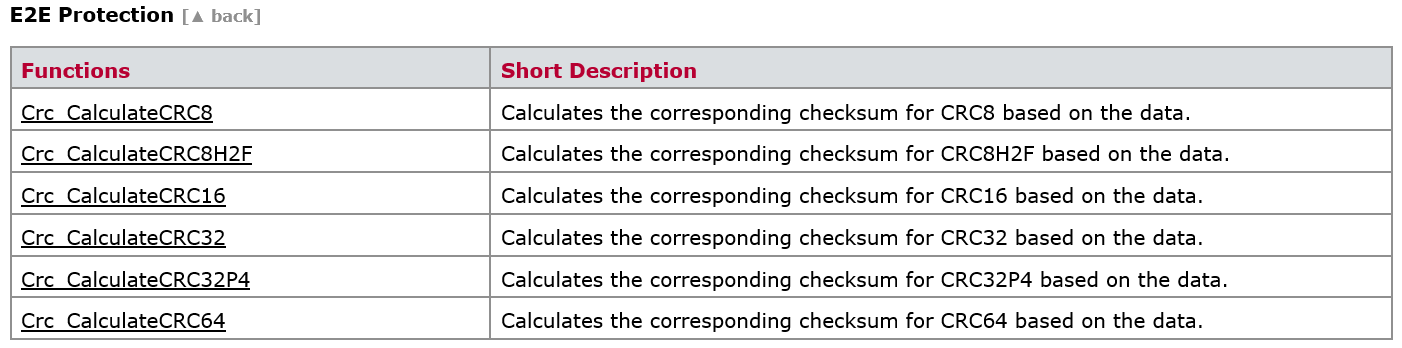
当然,如果你不想写代码,capl中提供了现成的函数来计算不同的CRC校验和
又或者你也可以使用CRC在线计算器
CRC(循环冗余校验)在线计算
 IDEA激活码
IDEA激活码


