本系列文章【数据结构与算法】所有完整代码已上传 github,想要完整代码的小伙伴可以直接去那获取,可以的话欢迎点个Star哦~下面放上跳转链接
本篇文章来讲解一下更高级的排序算法,顾名思义,它们的排序思想一定更复杂,效率也一定比简单排序更高。为了更方便地理解高级排序算法,还是建议大家先把简单排序了解清楚,因为高级排序也多少借鉴了简单排序的思想,下面放上文章链接
【数据结构与算法】简单排序(冒泡排序、选择排序、插入排序)完整思路,并用代码封装排序函数
那么就让我们来了解一下三种高级排序算法吧
一、希尔排序
希尔排序是插入排序的改进版本,弥补了插入排序在某些情况下的缺点。
例如,当长度为100的数组,前面有序区域的数组长度为80,此时我们用第81个数去跟前面有序区域的所有元素比较大小,但恰巧第81个数又是这100个数里最小的,它本应该在索引为1的位置,如图所示
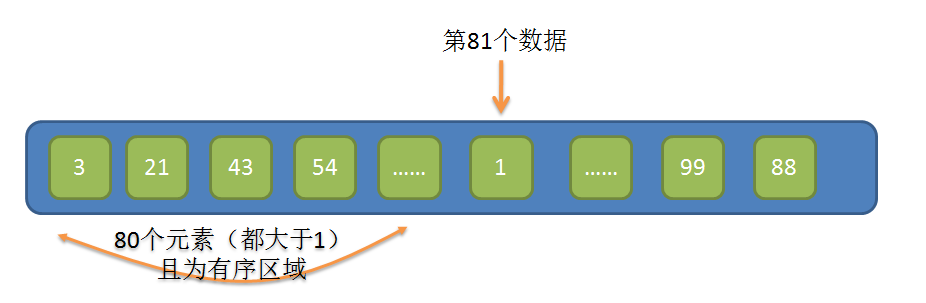
本例中第81个数据的值为1,那么前面有序区域里的80个元素都要往后移动一个位置,这种情况就非常影响排序性能。
因此,我们就要想办法尽可能早点让小的值靠前,让大的值靠后,这样就能避免上述情况了,这就是希尔排序要解决的问题。
希尔排序也叫做缩小增量排序,它通过先设置一个增量n,大小为数组长度的一半,将间隔为n的元素视作一个组,然后对每个组内部的元素进行从小到大进行插入排序;然后再将增量n缩小一半,再次进行分组插入排序,直到增量n为1,因为增量为1的时候,所有的元素都为同一个组了
为了方便大家理解,我用一个例子来展示一个完整的希尔排序过程,首先数据的初始状态如图所示,这里为了更好地体现希尔排序的优点,我特地把值较大的元素放到了靠左的位置,把值较小的元素放到了靠右的位置

该数组长度为8,因此我们设置初始的增量为 8 / 2 = 4,那么该数组的分组情况如下图所示:

图中颜色相同的元素为一组,每组内的各个元素间隔都为4,现在对每个组内进行从小到大排序,排序结果如下图所示:

此时我们将增量缩小一半,即 4 / 2 = 2,同样的,现在将所有元素重新组合,把所有间隔为2的元素视作一组,分组结果如下图所示:

图中颜色相同的元素为一组,每组内的各个元素间隔都为2,现在对每个组内进行从小到大排序,排序结果如下图所示:

我们继续将增量缩小一半,即 2 / 2 = 1,同样的,现在将所有元素重新组合,把所有间隔为1的元素视作一组,此时所有的元素都为同一组了,就相当于对所有的数据进行普通的插入排序,我们可以看到,对比最开始的数据,总得来说,小的值都比较靠左了,大的值也都比较靠右了,这样排序起来效率就很高了。结果如下图所示:

接下来用一个动图,演示一下完整的希尔排序全过程

了解完了希尔排序的实现过程,我们现在用代码来封装一下
function shellSort(arr) {
// 1. 获取数组长度
let length = arr.length
// 2.获取初始的间隔长度
let interval = Math.floor(length / 2)
// 3. 不断地缩小间隔的大小,进行分组插入排序
while(interval >= 1) {
// 4. 从 arr[interval] 开始往后遍历,将遍历到的数据与其小组进行插入排序
for(let i = interval; i < length; i++) {
let temp = arr[i]
let j = i
while(arr[j - interval] > temp && j - interval >= 0) {
arr[j] = arr[j - interval]
j -= interval
}
arr[j] = temp
}
// 5. 缩小间隔
interval = Math.floor(interval / 2)
}
return arr
}
来用刚才举得例子来验证一下我们封装的希尔排序是否正确
let arr = [63, 76, 13, 44, 91, 8, 82, 3]
let res = shellSort(arr)
console.log(res)
/* 打印结果 [3, 8, 13, 44, 63, 76, 82, 91] */
上述情况中,希尔排序最坏情况下的时间复杂度为O(n²)。其实希尔排序的时间复杂度跟增量也有关系,我们上面是通过数组长度一直取一半获取的增量,其实还有一些别的增量规则,可以使得希尔排序的效率更高,例如Hibbard增量序列、Sedgewick增量序列,本文就不对这两种增量做过多的讲解了,大家可以去网上搜索一下。
二、归并排序
归并排序的实现是使用了一种分而治之的思想,即将一个数组不断地通过两两分组的方式进行比较大小,最后直到所有元素都被分到一组里,那自然就是整体有序的了。
我们来看一下归并排序的主要思路,首先有如下图所示排列的一组数据:

首先从左往右,每两个元素视为一组,组合前要分别判断一下这两个元素的大小,小的在左,大的右,如图所示

继续再取两个元素组成一组并比较大小,如图所示:

继续上一个步骤,如图所示:

此时,原数组的所有元素都被两两分组完毕了,现在整个数组的长度变成了3,如下图所示:

此时,我们要重新从左向右,每次取两个元素组成一组,同时分别比较两个元素内的所有子元素的大小,因为此时的两个元素内部是有序的,所以我们比较两者大小的话,只需要每次比较数组的第一个元素即可,过程如下图所示:

此时原数组中只剩下一个元素了,所以就不对其做任何组合处理了,此时的数组是这样的:
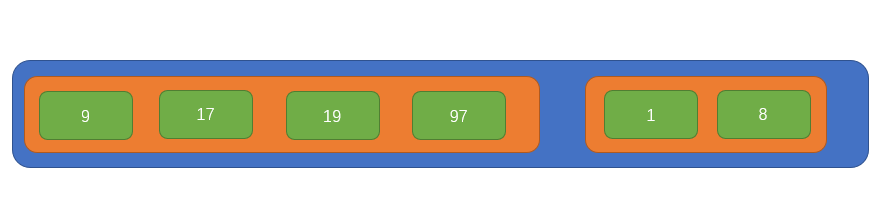
此时的数组内只有两个元素了,所以我们只需要不断比较两个元素内部的子元素大小,即可获得完整的有序数组了,过程如下图所示:

这就是一个完整的归并排序的过程,接下来我们用代码来实现一下吧
function mergeSort(arr) {
// 将所有元素不断地两两组合,直到所有元素都被组合成一个组
while(arr.length > 1){
// 获取一下遍历前的数组长度,方便下面判断需要组合几次
let length = arr.length
// 创建空的新数组,用于存放所有组合后的元素
let next_arr = []
// 取两个元素进行组合,一共取 length / 2 次
for(let i = 0; i < Math.floor(length / 2); i++){
// 取出第一个元素
let left = [].concat(arr.shift())
// 取出第二个元素
let right = [].concat(arr.shift())
// 创建另一个新的空数组,用于存放组合后的所有元素
let new_arr = []
// 取两个数组中头部最小的值放到新数组中,直到一个数组为空
while(left.length > 0 && right.length > 0){
let min = left[0] > right[0]? right.shift() : left.shift()
new_arr.push(min)
}
// 将合并好的数组添加到新的数组中
next_arr.push(new_arr.concat(left.length == 0? right : left))
}
// 判断是否有一个未成组的数组
if(arr.length == 1) next_arr.push(arr[0]);
// 将所有组合后的元素构成的新数组作为下一次遍历的对象
arr = next_arr
}
// 返回完整有序数组
return arr[0]
}
我们来使用一下该方法,看看是否正确,为了方便大家理解,我在归并排序的函数里加了一条打印的代码,可以看到每次遍历后的数组情况,结果如下
let arr = [19, 97, 9, 17, 1, 8]
mergeSort(arr)
/* 打印结果: 第一次组合后:[ [ 19, 97 ], [ 9, 17 ], [ 1, 8 ] ] 第二次组合后:[ [ 9, 17, 19, 97 ], [ 1, 8 ] ] 第三次组合后:[ [ 1, 8, 9, 17, 19, 97 ] ] */
查看代码我们不难发现,归并排序运行起来非常得占内存,因为在组合的过程中,我们不断得在创建新的数组,然后又进行合并。但其比较次数却非常得少,只在每次合并元素时进行比较,因此归并排序的效率还是非常得高的。
三、快速排序
快速排序相信大家一定不陌生,就算没用过也一定听过,拥有这么大的名声,那么它的排序效率一定很高。而且快速排序也是面试中经常会被问到的,可能会让你当场手写哦~所以大家一定要掌握它的核心思想
快速排序也用到了分而治之的思想,它的实现思路非常得有意思:
- 先选一个元素作为基点pivot
- 将其余元素中所有比pivot小的值放到pivot的左边;将所有比pivot大的值放到pivot的右边
- 然后分别对pivot左边的所有元素、pivot右边的所有元素从步骤1开始排序依次,直到所有元素完整有序
思路看着很简单,那么我们来用一个例子具体看一下快速排序的全过程吧
首先有这样一组数据,如下图所示:

首先我们要选取一个元素作为基点pivot,最后排序完后,pivot左边的所有元素都是小于pivot的,右边的所有元素都是大于pivot的,因此我们希望的是尽量是两边平均一下,所以这里将采用一种方式寻找到一个大概的中点,即取数组两头的索引,分别为left 、right,再取一个中点 center,结果如下图:
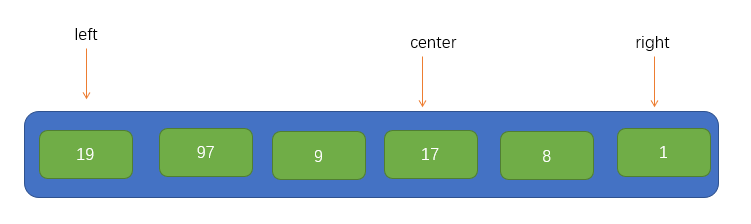
然后在这三个元素中找到一个中等大小的值,并将其放到数组的开头位置,如下图所示:

到此,我们就可以将该数组的第一个元素作为此次遍历的基点pivot了,同时,我们将引入两个指针,即 i 和 j,分别指向 left 和 right,如图所示
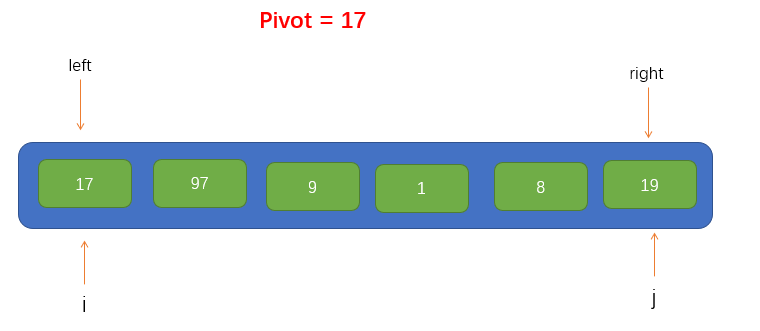
接下来就可以进行遍历了,这里我们把遍历过程称为填坑法,因为现在我们取到了数组的第一个值为pivot,所以可以假设这个位置上没有元素了,留了一个坑,需要我们将别的元素填进来。所以我们要从指针 j 开始往右寻找到一个比pivot小的值,若找到了,则将找到的值填到坑里,但要注意的是,指针 j 不能找到 指针 i 的左边去,即当指针 j 与 指针 i 重合时就停止移动。
过程如下图所示:

此时我们可以看到,指针 j 找到了一个小于pivot的值 8,并将找到的值填到了坑里,那么此时指针 j 所指向的位置就留下了一个坑,又需要别的元素来填坑,所以此时我们就要让指针 i 向右找一个大于pivot的值,并将值填到坑里,同样的,指针 i 也不能找到指针 j 的右边,即当指针 i 与 指针 j 重合时就停止移动。
过程如下图所示:

指针 i 找到了一个大于pivot的值 97 并将其填到了坑里,此时指针 i 所在的位置就留下了一个坑,因此我们又要让指针 j 往左找小于pivot的值并填到坑里,过程如图所示:

紧接着,指针 i 又要向右找大于pivot的值,但是移动了两个位置都没有找到,并且此时指针 i 指针 j 重合了,此时我们只需要将pivot填入到坑里就实现了pivot左边的所有元素小于它,右边所有的元素都大于它了,如图所示:

接下来的操作,就是我们要单独对此时pivot的左边所有元素和右边的所有元素进行上述的一系列操作,就可以实现快速排序了。本例中的左右两边区域的元素个数都是小于等于3个的,因此直接将这几个值互相进行比较大小比较方便,过程如下图:

了解了快速排序的实现思路,我们来用代码来实现一下
function quickSort(arr) {
// 两个数据进行交换
function exchange(v1, v2) {
let temp = arr[v1]
arr[v1] = arr[v2]
arr[v2] = temp
}
// 找到相对合适的元素放到数组索引为0的位置作为基点pivot
function init(left, right) {
let center = Math.floor((left + right) / 2)
// 比较索引为left、center、right三个值的大小,从小到大排列
if(arr[left] > arr[right]) exchange(left, right)
if(arr[center] > arr[right]) exchange(center, right)
if(arr[left] > arr[center]) exchange(left, center)
// 判断数组长度是否大于3,若小于3,则数组已经排序好了,不需要做任何处理
if(right - left > 2) exchange(left, center)
}
function quick(left, right) {
init(left, right)
// 若数组长度小于等于2,则不需要做任何操作了,因为init函数已经排序好了
if(right - left <= 2) return;
// 创建指针i和j,分别指向left和right
let i = left
let j = right
// 将该数组区域的第一个元素作为基点pivot
let pivot = arr[i]
// 不断让指针i和j寻找合适的值填坑,直到两个指针重合
while(i < j) {
// 指针j不断向左找小于pivot的值,但指针j不能找到指针i的左边
while(arr[j] > pivot && j > i) {
j --
}
// 将找到的小于pivot的值填到指针i所指向的坑中
arr[i] = arr[j]
// 指针i不断向右找大于pivot的值,但指针i不能找到指针j的右边
while(arr[i] < pivot && i < j) {
i ++
}
// 将找到的大于pivot的值填到指针j所指向的坑中
arr[j] = arr[i]
}
// 将pivot填到指针i和指针j共同指向的坑中
arr[i] = pivot
// 对此时pivot的左边所有元素进行快排
quick(left, i - 1)
// 对此时pivot的右边所有元素进行快排
quick(i + 1, right)
}
quick(0, arr.length - 1)
return arr
}
我们可以简单来验证一下快速排序的正确性
let arr = [19, 97, 9, 17, 8, 1]
console.log(quickSort(arr))
/* 打印结果为: [1, 8, 9, 17, 19, 97] */
四、结束语
排序算法中的高级排序(希尔排序、归并排序、快速排序)就已经讲完啦,下一篇文章为动态规划
我是Lpyexplore,一个因Python爬虫而进入前端的探索者。创作不易,喜欢的加个关注,点个收藏,给个赞~
 IDEA激活码
IDEA激活码


