题目:
假设你是一个小偷,有一个可放总重量为m(m<1000)的背包。现有n(n<32)件物品。
总量分别为W1,W2,...,Wn。并且,物品具有价值,分别为V1,V2,...,Vn。m、n、Wi(1=<i<=n)均为正整数,
并且,每种物品的数量不限,也就是说你可以重复拿一种物品。求能装入的最大总价值。
输入格式:
第一行为两个正整数m和n
接下来n行分别为n对整数,分别表示该物品的重量和价值。
Example:
Input:
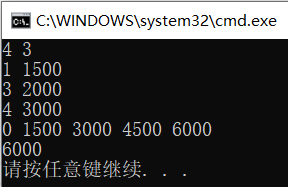
4 3
1 1500
3 2000
4 3000
Output:
6000
输入
6 3
2 3
4 7
3 6
输出
12
【分析】
相较于上一篇动态规划-完全背包(含全部代码),我们把空间复杂度降低了。下表为未优化的dp空间。
| 第i件物品\背包重量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 (2,3) | 0 | 0 | 3 | 3 | 6 | 6 | 9 |
| 2(4,7) | 0 | 0 | 3 | 3 | 7 | 7 | 10 |
| 3(3,6) | 0 | 0 | 3 | 6 | 7 | 9 | 12 |
由于dp[i][j]与dp[i-1][j]和dp[i][j-W[i]]有关,因此,我们只需一行即可,计算第i次dp[j]时,当前dp[j]存的就是上一次的dp[j],当前dp[j-W[i]]已经是更新后的了,因为j从小到大更新,j-W[i]必小于j。
代码:
/*
Project: dp_fullback_better
Date: 2019/01/11
Author: Frank Yu
题目:假设你是一个小偷,有一个可放总重量为m(m<1000)的背包。现有n(n<32)件物品。
总量分别为W1,W2,...,Wn。并且,物品具有价值,分别为V1,V2,...,Vn。m、n、Wi(1=<i<=n)均为正整数,
并且,每种物品的数量不限,也就是说你可以重复拿一种物品。求能装入的最大总价值。
输入格式:
第一行为两个正整数m和n
接下来n行分别为n对整数,分别表示该物品的重量和价值。
Example:
Input:
4 3
1 1500
3 2000
4 3000
Output:
6000
【分析】
1.状态表示
dp[i][j] 表示前i件物品放入容量为j的背包的最大价值。
2.
状态转移方程:
dp[i][j] = dp[i-1][j],j<w[i],即背包无法装下第i件物品
dp[i][j] = max(dp[i-1][j],dp[i][j-W[i]]+V[i]),j>=W[i],即背包可以装下第i件物品。看装下后是否价值更高
3.边界条件
dp[i][0]=0,dp[0][j] = 0
输入
6 3
2 3
4 7
3 6
输出
12
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define maxm 1000
#define maxn 32
using namespace std;
int W[maxn], V[maxn];
//打印表
void display(int dp[maxm], int m)
{
for (int j = 0; j <= m; j++)
{
cout << dp[j] << " ";
}
cout << endl;
}
//主函数
int main()
{
int m, n;
int dp[maxm];
scanf("%d", &m);//背包重量
scanf("%d", &n);//物品种类
dp[0] = 0;
for (int i = 1; i <= n; i++)//下标即第几件物品,W[0]一直为0
{
scanf("%d", &W[i]);
scanf("%d", &V[i]);
}
//填表
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (j < W[i])
{
dp[j] = dp[j];
}
else {
dp[j] = max(dp[j], dp[j - W[i]] + V[i]);
}
display(dp,m);
cout << dp[m] << endl;
return 0;
}
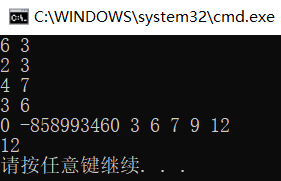
结果截图:
根据表格和我的初始化结果,读者想一想,为什么会出现-85893460呢?
 IDEA激活码
IDEA激活码