题目:假设你是一个小偷,有一个可放总重量为m(m<1000)的背包。现有n(n<32)件物品,总量分别为W1,W2,...Wn。
其中,m、n、Wi(1=<i<=n)均为正整数,现要求你尝试挑选几件物品,使这些物品重量之和为m。
若可以,输出那true。否则,输出false。
输入格式:
第一行为两个正整数m和n
第二行为n个正整数,分别表示n件物品的重量。
Example:
Input:
10 5
1 2 3 4 5
Output:
true
【分析】将n件物品放到数组W[n+1]中,二叉树思想(选或不选思想),函数recu_simple_back(m,n),如果选择第n个物品,且Wn=m,则装满。
如果Wn<m,且n>=1,则从剩下的n-1件物品中继续找,即recu_simple_back(m-W[n],n-1)。
如果Wn>m,且n>=1,则不选第n件,即recu_simple_back(m,n-1)。
递归出口:成功(正好装满): m==0;
失败(背包已撑爆) m<0; //2019年01月12日更新
失败(无物品可选): n<1;
递归树分析(19年01月12日更新):

简单的想,本题的递归调用类似一颗二叉树,要么选,要么不选。有一条路返回True,就停止。
F(m,n)=F(m-W[n],n-1)||F(m,n-1),但是,这样的话,几乎要运行高度为n的二叉树所含结点个数个函数。那耗费时间巨大。
我们可不可以进行修剪呢?增加一些递归出口,或者用if进行判断,当然是可以的。
经过修改后,递归树如上图,我们找到了第1、4、5件物品。请看下方新结果截图,我们发现,修剪后,只运行了n个函数。相比于2^(n-1)个函数少了很多,从指数降到n,实现了质的飞跃。递归之所以慢,就是因为运行函数过多,进行修剪,时间就会逼近动态规划。当然,我也写了动态规划的代码。有兴趣的读者可以看看。
代码:
/*
Project: recu_simple_bag
Date: 2019/01/10
Author: Frank Yu
题目:假设你是一个小偷,有一个可放总重量为m(m<1000)的背包。现有n(n<32)件物品,总量分别为W1,W2,...Wn。
其中,m、n、Wi(1=<i<=n)均为正整数,现要求你尝试挑选几件物品,使这些物品重量之和为m。
若可以,输出那true。否则,输出false。
输入格式:
第一行为两个正整数m和n
第二行为n个正整数,分别表示n件物品的重量。
Example:
Input:
10 5
1 2 3 4 5
Output:
true
【分析】将n件物品放到数组W[n+1]中,二叉树思想(选或不选思想),函数recu_simple_back(m,n),如果选择第n个物品,且Wn=m,则装满。
如果Wn<m,且n>=1,则从剩下的n-1件物品中继续找,即recu_simple_back(m-W[n],n-1)。
如果Wn>m,且n>=1,则不选第n件,即recu_simple_back(m,n-1)。
递归出口:成功(正好装满): m==0;
失败(背包已撑爆) m<0; //2019年01月12日更新
失败(无物品可选): n<1;
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define maxn 33
using namespace std;
int W[maxn];//重量
//递归求解
bool recu_simple_back(int m, int n)
{
if (m == 0) return true;//成功找到
if(m < 0) return false;//修剪树,2019年01月12日更新
if (n<1) return false; //没有可选的物品了
if (recu_simple_back(m - W[n], n - 1))//装上物品n,且还有解
{
printf("%d if ",n);//调试用,2019年01月12日更新
return true;
}
else
{
printf("%d else ",n);//调试用,2019年01月12日更新
return recu_simple_back(m, n - 1);//不装该物品
}
}
//主函数
int main()
{
memset(W, 0, sizeof(W));//初始化
int m, n;//背包质量,物品件数
scanf("%d", &m);
scanf("%d", &n);
for (int i = 1;i <= n;i++)//下标即第几件物品,W[0]一直为0
{
scanf("%d", &W[i]);
}
if(recu_simple_back(m, n))
printf("true");
else printf("false");
return 0;
}结果截图:
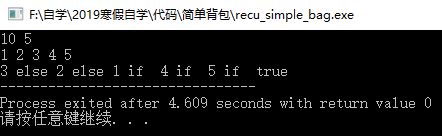
那么,问题来了,作为一个小偷,塞满了背包就行了吗?有没有点出息。难道像无名之辈里面似的,不考虑价值,偷一背包模型机呀。当然不,我们还要考虑价值,做有见识的小偷!
请看考虑物品价值的0/1背包问题:动态规划-0/1背包问题(含全部代码)
更多数据结构与算法实现:数据结构(严蔚敏版)与算法的实现(含全部代码)
 IDEA激活码
IDEA激活码


